Изучение зависимостей площадей и периметров в четырехугольниках
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Хакверди Елиз Уналовна 1
1Муниципальное бюджетное общеобразовательное учреждение “Средняя общеобразовательная школа №30”
Берговина Ю.Д. 1
1Муниципальное бюджетное общеобразовательное учреждение “Средняя общеобразовательная школа №30”
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
С понятием периметр и площадь я познакомилась в 3 классе. Эти важные понятия необходимы человеку на протяжении всей его жизни. Деятельность строителей, инженеров, земледельцев и представителей других профессий немыслима без прочных знаний по этой теме.
Актуальность темы. Понятия «площади» и «периметра» необходимы человеку в окружающей жизни постоянно, например – сделать ремонт в доме или красиво оформить клумбу на даче. И то и другое понятие связывают стороны многоугольников. Знание зависимостей между этими величинами очень важно для современного человека.
Цель проекта: установить некоторые зависимости между площадью и периметром, увидеть их применение в практических ситуациях.
Задачи:повторить понятия по теме исследования, а именно: «площадь фигуры» и «периметр фигуры»; провести необходимые исследования и опыты; сделать выводы о зависимости площадей и периметров; рассмотреть практическое применение полученных результатов.
Основнаячасть
Определение предмета исследования. Что нужно выяснить:
Как связаны периметры и площади прямоугольников?
Зависит ли площадь прямоугольника от его периметра?
Какой прямоугольник имеет наибольшую площадь при заданном периметре?
Если известен периметр прямоугольника, то нельзя ли однозначно установить его площадь?
Что можно сказать о зависимости площади квадрата от его периметра?
Проблема.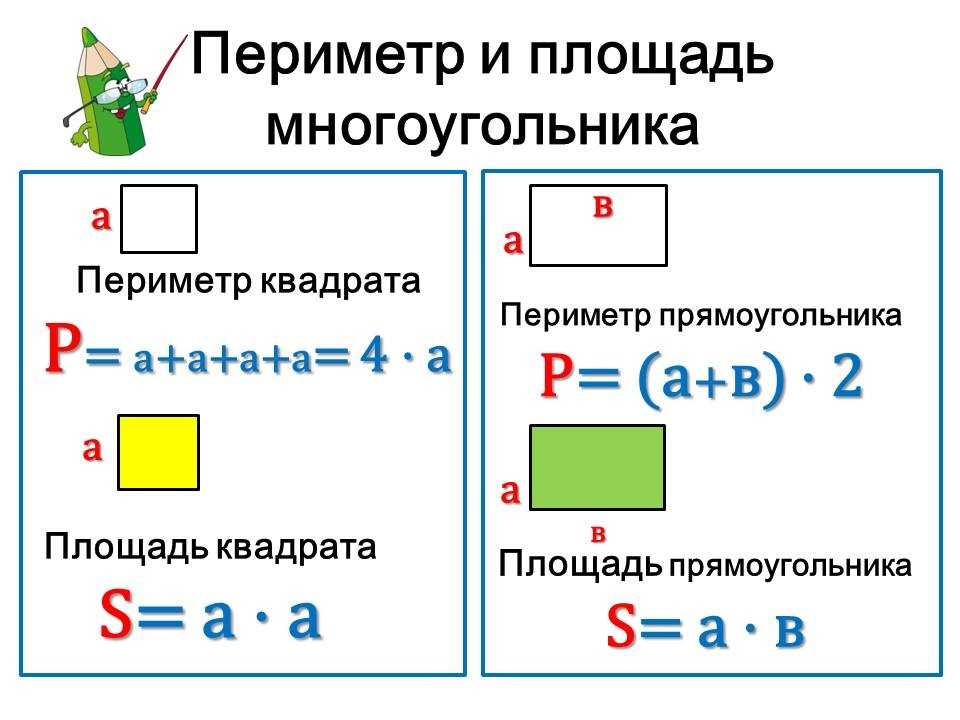
Никаких зависимостей связывающих площади и периметры фигур мы пока не изучили.
Вот, самый простой пример, который задает проблему: «Есть два участка земли 80 м на 100 м и 50 м на 160 м. Вроде, площадь одинаковая – 8000 м 2, а первый участок выгоднее купить, чем второй, забор то на 60 м короче строить». С точки зрения математики, все ясно, а вот логически – странно, периметр это замкнутая воображаемая нить, и то, что внутри нее не должно меняться, как ее не крути. Почему есть разница в периметрах? Так все-таки, есть ли какие-то зависимости, или площадь и периметр никак не зависят друг от друга?
Гипотеза.Предполагаем, что некоторые зависимости существуют. С изменением длины одной из сторон прямоугольника при заданном периметре изменится и площадь этого прямоугольника. Можно даже предположить, что если площадь больше, то периметр больше. Если у одной фигуры больше периметр, чем у второй, то её площадь больше, меньше или по-разному?
Мы уже знаем:
Периметр – величина, равная сумме длин всех сторон многоугольника.
Площадь фигуры – величина, показывающая сколько места занимает фигура на плоскости.
Свойства площадей нам тоже известны:
Равные фигуры имеют равные площади.
Площадь всей фигуры равна сумме площадей ее частей.
За единицу площади принимают площадь квадрата, сторона которого равна единичному отрезку.
Проверка гипотезы.
Исследования начнем с простой и хорошо знакомой нам фигуры – прямоугольника.
Исследование №1.
Заполним таблицу, считая площадь одной клеточки равной 1 см 2
Таблица №1
|
№ |
Фигуры |
Площадь (S, см 2) |
Периметр |
|
1 |
1 |
4 |
|
|
2 |
2 |
6 |
|
|
3 |
3 |
8 |
|
|
4 |
4 |
10 |
|
|
5 |
4 |
8 |
|
|
6 |
5 |
12 |
|
|
7 |
6 |
14 |
|
|
8 |
6 |
10 |
|
|
9 |
7 |
16 |
|
|
10 |
8 |
12 |
|
|
11 |
8 |
18 |
|
|
12 |
9 |
20 |
|
|
13 |
9 |
12 |
|
|
14 |
10 |
22 |
|
|
15 |
10 |
14 |
Исследуя результаты измерений, делаем вывод, что не всегда увеличение площади означает, что периметр тоже увеличивается, например фигуры №3 и №5 или фигуры №4 и №8, или фигуры №6 и №10 и №13.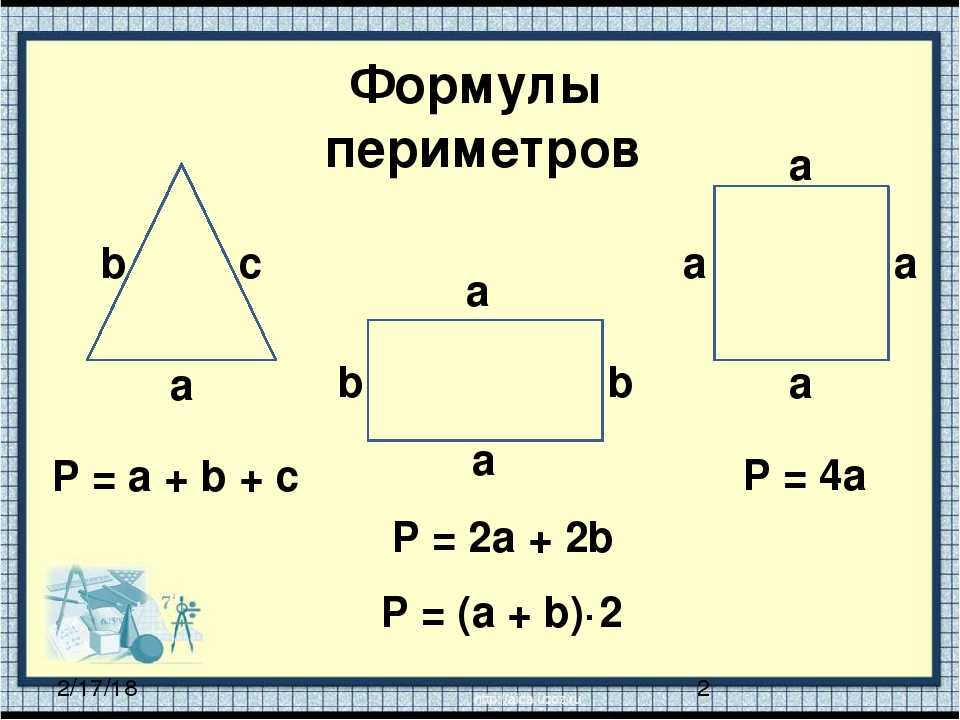
Мы заметили, если периметр одного прямоугольника больше, то и его площадь больше чем у других, например фигуры №2 и №3 или фигуры №4 и №6. Однако, если периметр одного прямоугольника больше, то его площадь не всегда больше, например фигуры №6 и №8.
При одинаковом периметре и площади бывают разные! Отчего же так происходит?
Продолжим наблюдения.
Исследование №2.
Таблица №2
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см |
Периметр (Р, см) |
|
1 |
1 |
100 |
100 |
202 |
|
2 |
2 |
50 |
100 |
104 |
|
3 |
4 |
25 |
100 |
58 |
|
4 |
5 |
20 |
100 |
50 |
|
5 |
10 |
10 |
100 |
40 |
|
6 |
20 |
5 |
100 |
50 |
|
7 |
25 |
4 |
100 |
58 |
|
8 |
50 |
2 |
100 |
104 |
|
9 |
100 |
1 |
100 |
202 |
Замечаем, что при равных площадях периметры не равны, самый маленький периметр из всех прямоугольников с равными площадями – у квадрата.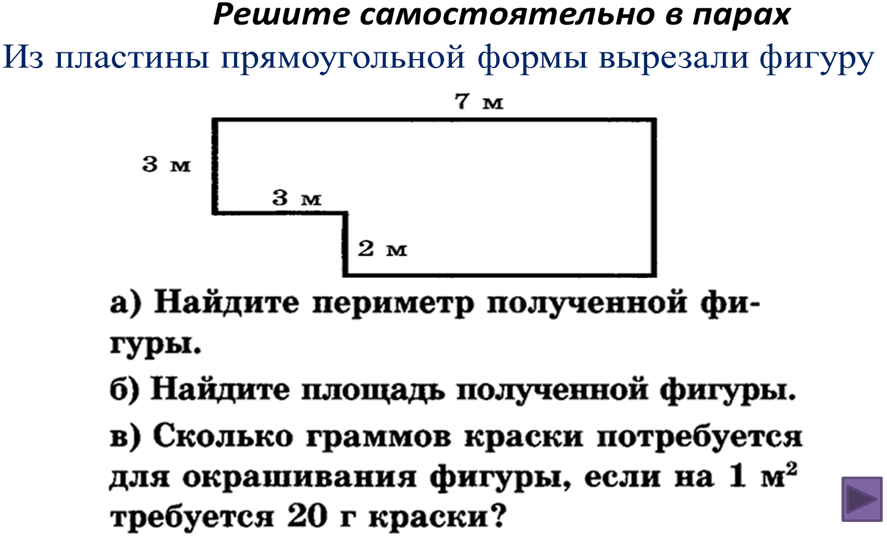
Вот какое замечательное свойство у квадрата! Оказывается, что среди всех прямоугольников одинаковой площади у квадрата самый маленький периметр!
Какой же из всех прямоугольников заданного периметра имеет наибольшую площадь? Решение этой задачи было известно ещё математикам Древней Греции. Оно изложено в книге Евклида.
Исследование №3.
Таблица №3
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
1 |
49 |
49 |
100 |
|
2 |
2 |
48 |
96 |
100 |
|
3 |
5 |
45 |
225 |
100 |
|
4 |
10 |
40 |
400 |
100 |
|
5 |
20 |
30 |
600 |
100 |
|
6 |
25 |
25 |
625 |
100 |
Очевидно, можно сделать вывод, что при одинаковом периметре, самая выгодная площадь у квадрата.
Запомним это замечательное свойство квадрата, заключать в своих границах наибольшую площадь при постоянном периметре. Отчего же возникают такие зависимости, в чем причина? Чтобы лучше разобраться в этом вопросе, проведем опыт.
Опыт.
Я взяла четырехугольник – квадрат. Измерила его стороны, вычислила площадь и периметр. Разрезала фигуру пополам и составила новую фигуру (Приложение 2, стр.17). Результаты измерений занесла в таблицу №4.
Таблица №4
|
№ фигуры |
1 сторона (длина, см) |
2 сторона (ширина, см) |
Площадь (S, см 2) |
Периметр (Р, см) |
|
1 |
8 |
8 |
64 |
32 |
|
2 |
16 |
4 |
64 |
40 |
Таблица №5
|
1 фигура |
|
|
2 фигура |
Количество квадратиков не изменилось.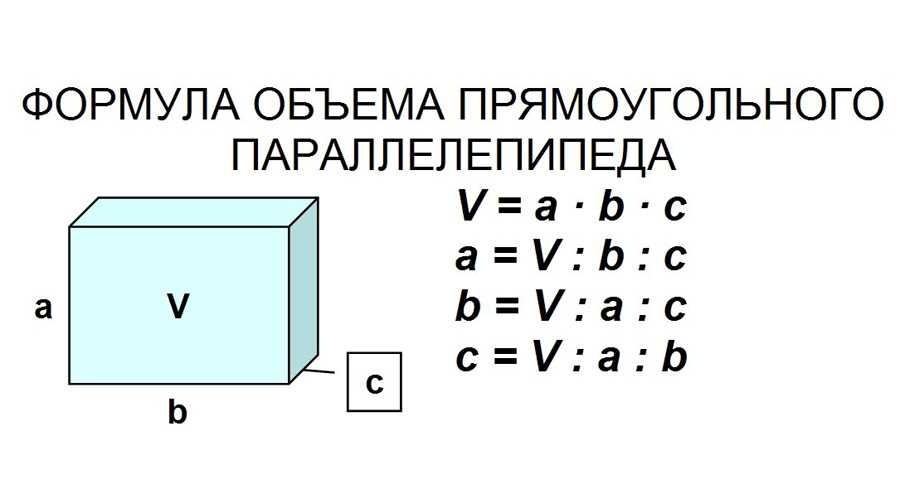
Наблюдаем, что происходит со сторонами, когда периметр увеличивается. У фигуры появились дополнительные стороны, которые стали границами, это дополнительные 8+8=16 см, и исчезла граница 4+4=8 см. Итого: 16-8=8 см. Вот и дополнительные 8 см. Периметр увеличится.
Практические задачи.
А что можно сказать о зависимости площади квадрата от его периметра?
Задача №1. Если известен периметр квадрата, то можно ли однозначно установить его площадь?
Решим задачу для квадрата, периметр которого равен 40 см. Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.
1) 40 : 4 = 10 (см) – одна сторона
2) 10 • 10 = 100 (см 2) – площадь
Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.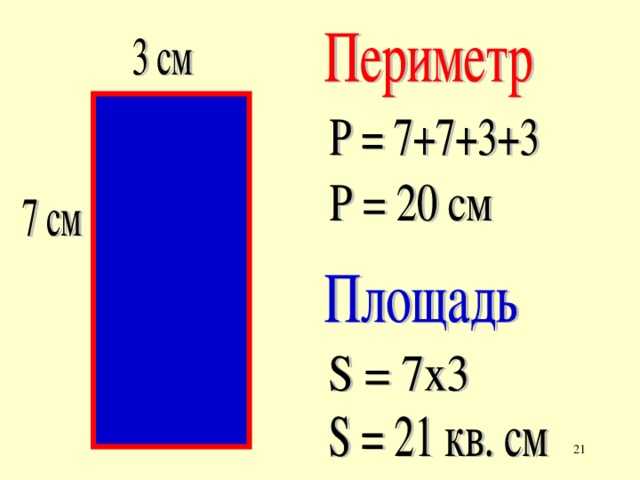
Задача №2. Начертите какой-нибудь квадрат. Как надо изменить его стороны, чтобы построить квадрат, площадь которого была бы: 1) в 4 раза больше? 2) в 9 раз больше? 3) в 16 раз больше?
Проверим решение построением (Приложение 3, стр.18).
Таблица №6
|
№ |
Фигуры |
Вывод |
|
1 |
Стороны увеличить в 2 раза |
|
|
2 |
Стороны увеличить в 3 раза |
|
|
3 |
Стороны увеличить в 4 раза |
Задача №3.
Начертите три прямоугольника, у одного из которых стороны имеют длину 7 см и 3 см, у второго соответственно 8 см и 2 см, а у третьего – 9 см и 1 см. Вычислите периметр и площадь каждого из этих прямоугольников. Сравните получившиеся периметры между собой и получившиеся площади между собой.
Проиллюстрируем на примере.
Первый прямоугольник: Р = (7 + 3) • 2 = 20 (см), S = 7 • 3= 21 (см 2).
Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (см 2).
Третий прямоугольник: Р = (9 + 1) • 2 = 20 (см), S = 9 • 1 = 9 (см 2).
Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника и площадь второго – больше площади третьего: 21 > 16 > 9 . Если известен периметр прямоугольника, то нельзя однозначно установить его площадь. Площадь прямоугольника не будет однозначно зависеть от его периметра.
А, что можно сказать о зависимости периметра квадрата от длины его стороны?
Задача №4. Может ли периметр квадрата не измениться, если длина стороны квадрата изменилась? Могут ли получиться разные значения периметра квадрата при одном и том же значении длины его стороны?
Таблица №7
|
Длина стороны квадрата α, см |
1 |
2 |
3 |
4 |
5 |
|
Периметр квадрата Р, см |
4 |
8 |
12 |
16 |
20 |
Из таблицы видно, что с изменением стороны квадрата изменяется и периметр.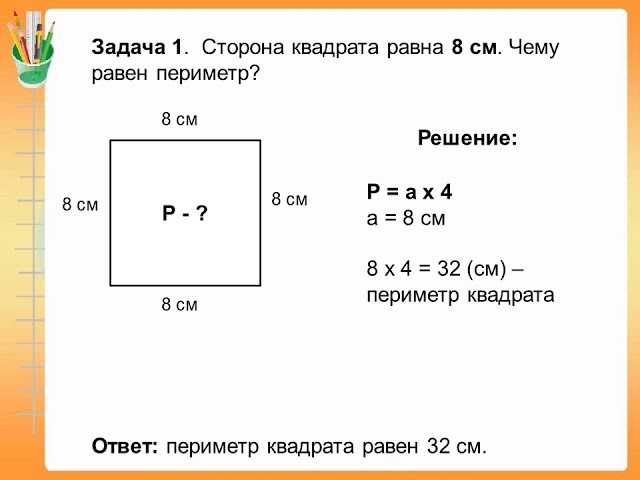
Периметр квадрата однозначно зависит от длины его стороны, поскольку периметр квадрата – 4 • α, то есть при изменении значения α, изменится значение выражения. Если изменить длину стороны квадрата, то это обязательно приведёт к изменению его периметра, то есть Р зависит от а.
Если длина стороны квадрата увеличивается, то его периметр тоже увеличивается.
Если длина стороны квадрата уменьшается, то его периметр тоже уменьшается.
Заключение
Практические результаты и выводы, полученные мною, могут быть использованы при подготовке домашних заданий и в бытовых вопросах, постоянно возникающих в жизни. Мои исследования помогли узнать о том, что по известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
Я выяснила, что площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.
Основные выводы.
Если периметры прямоугольников равны, то площади могут быть различны.
Не всегда увеличение площади прямоугольников означает, что периметр тоже увеличивается.
Если площади прямоугольников равны, то периметры могут быть различны.
Из всех прямоугольников с равными площадями наименьший периметр имеет квадрат.
Из всех прямоугольников с равными периметрами наибольшую площадь имеет квадрат.
Площадь квадрата однозначно зависит от его периметра.
Основные выводы я разместила на памятках-закладках (Приложение 4.1 и 4.2, стр.19-20)
Списокиспользованныхисточниковилитературы
А. Г. Мерзляк. Математика: 5 кл.: учебник для общеобразовательных организаций / А.
Г. Мерзляк, В. Б. Полонский, М. С. Якир. − 2-е изд., перераб. – М.: Вентана-Граф, 2018
М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, Математика – 4 класс, учебник для общеобразовательных организаций, в двух частях, М: Просвещение, 2018 г.-148 с.
3. Я.И. Перельман, Занимательная геометрия, Изд.: Терра-Книжный клуб, 2008 г., 384 стр.
4. Я.И. Перельман: Занимательная геометрия на вольном воздухе и дома , Издательство: Центрополиграф, 2017 г.
5. М.Г. Нефедова, Рабочая тетрадь по математике, Периметр и площадь – 3-4 классы. М: Издательство «Экзамен», 2014 г.- 46 стр.
6. М.И. Башмаков, М.Г. Нефедова, Математика, 3 класс, учебник, АСТ-Астрель, Москва, 2010 г.
7. О.В. Узорова, М.Г. Нефедова: Математика. 4 класс. Простые и составные задачи площади и периметра, Тренинговая тетрадь, ФГОС: издательства АСТ, 2015 г.
Приложение 4.1
Приложение 4.2
Просмотров работы: 6951
Фракталы (Федер Е.)
Фракталы (Федер Е.)
ОглавлениеПредисловиеГлава 1. 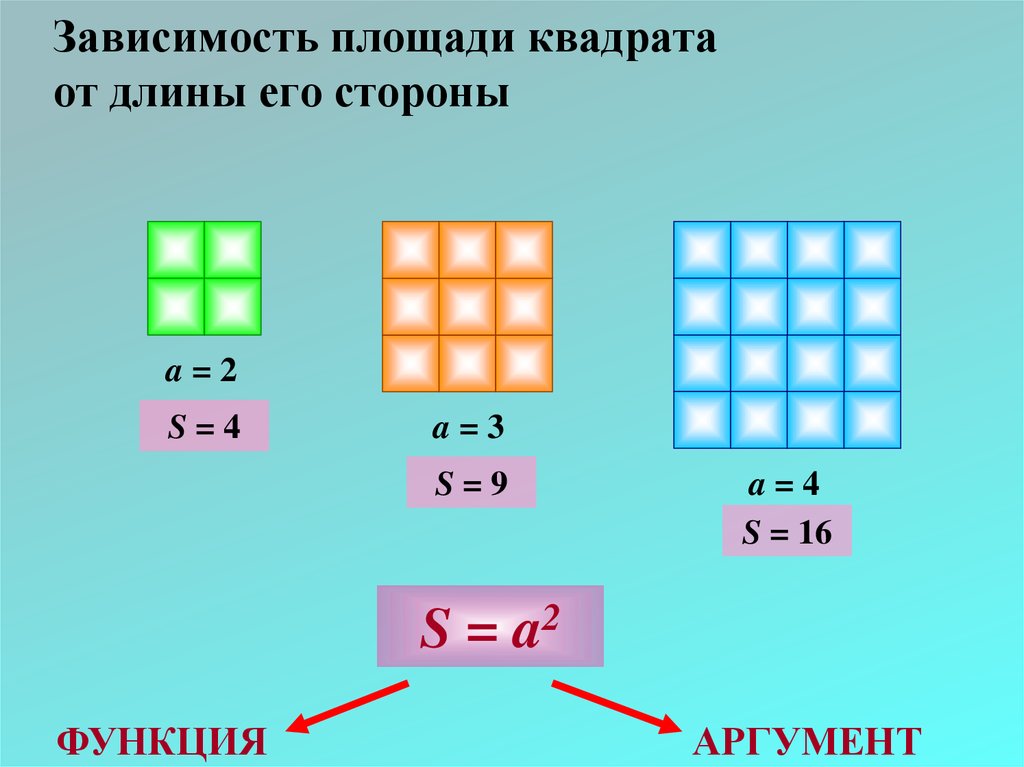 ВведениеГлава 2. Фрактальная размерность 2.2. Парадокс Шварца с площадью боковой поверхности цилиндра 2.3. Фрактальная размерность 2.4. Триадная кривая Кох 2.5. Подобие и скейлинг 2.6. Кривые Мандельброта-Гивена и Серпинского 2.7. Еще о скейлинге 2.8. Функция Вейерштрасса-Мандельброта Глава 3. Фрактальная размерность кластеров 3.1. Измерения фрактальных размерностей кластеров Глава 4. Образование вязких пальцев в пористых средах 4.1. Течение жидкости в ячейке Хеле-Шоу 4.2. Вязкие пальцы в ячейках Хеле-Шоу 4.3. Вязкие пальцы в двумерных пористых средах 4.4. Образование вязких пальцев и ОДА 4.5. Вязкие пальцы в трехмерных пористых средах Глава 5. Канторовские множества 5.1. Триадное канторовское множество 5.2. Скейлинг с неравными отношениями Глава 6. Мультифрактальные меры 6.1. Свертывание и чертова лестница 6.2. Биномиальный мультипликативный процесс 6.3. Фрактальные подмножества 6.4. Показатель Липшица-Гёльдера a 6.  5. Кривая f(a)6.6. Концентрация меры 6.7. Последовательность показателей массы t(q) 6.8. Соотношение между t(q) и f(a) 6.9. Свертывание с несколькими масштабами длины 6.10. Мультифрактальная конвекция Рэлея-Бенара 6.11. ОДА и гармонические меры 6.12. Мультифрактальный рост вязких пальцев Глава 7. Протекание 7.1. Протекание от узла к узлу на квадратной решетке 7.2. Бесконечный кластер при … 7.3. Самоподобие перколяционных кластеров 7.4. Конечные кластеры при протекании 7.5. Распределение величины кластеров при … 7.6. Корреляционная длина 7.7. Остов перколяционного кластера 7.8. Перколяция с вытеснением 7.9. Фрактальный диффузионный фронт Глава 8. Фрактальные временные ряды 8.1. Эмпирический закон Херста и метод нормированного размаха 8.2. Моделирование случайных рядов 8.3. Моделирование долговременных изменений Глава 9. Случайное блуждание и фракталы 9.2. Одномерное случайное блуждание 9.3. Свойства подобия одномерных случайных блужданий 9.  4. Обобщенное броуновское движение9.5. Определение обобщенного броуновского движения 9.6. Моделирование обобщенного броуновского движения 9.7. Метод R/S для обобщенного броуновского движения 9.8. Последовательные случайные сложения Глава 10. Самоподобие и самоаффинность 10.1. Стратегия смелой игры Глава 11. Статистика высоты волн 11.1. Метод R/S для наблюдений 11.2. R/S для данных, очищенных от сезонных вариаций Глава 12. Соотношение периметра и площади 12.1. Фрактальная размерность облаков 12.2. Фрактальная размерность рек Глава 13. Фрактальные поверхности 13.1. Фрактальная поверхность Кох 13.2. Поверхности случайного переноса 13.3. Построение фрактальных поверхностей 13.4. Поверхности случайного сложения 13.5. Комментарии к фрактальным пейзажам Глава 14. Исследования фрактальных поверхностей 14.2. Фрактальная размерность ландшафтов и параметров окружающей среды 14.3. Молекулярные фрактальные поверхности |
Площадь и периметр
В этой статье мы узнаем больше о том, как вычислить периметр и площадь четырехугольников, таких как квадраты и прямоугольники.
Периметры:
Длина границы замкнутой фигуры называется периметром плоской фигуры. Единицы периметра такие же, как и длина, например, метры, сантиметры, миллиметры и т. д.
Площадь:
Часть плоскости, ограниченная простой замкнутой фигурой, называется плоской областью, а измерение замкнутой плоской области называется площадью.
Площадь измеряется в квадратных единицах.
Связанные темы
- Периметры и площади прямоугольников
- Периметры и площади квадратов
- Периметр: определение длин отсутствующих сторон
- Как найти периметр многоугольников?
Прямоугольники:
Прямоугольники — это параллелограммы, имеющие \(4\) прямых углов. Все прямоугольники также являются параллелограммами, однако не все параллелограммы являются прямоугольниками.
Периметр \(P\) прямоугольника определяется по формуле \(P=2l+2w\), где \(l\) – длина, а \(w\) – ширина прямоугольника.
Площадь \(A\) прямоугольника рассчитывается по формуле \(A=lw\), где \(l\) – длина, а \(w\) – ширина.
Квадраты:
Квадраты — это четырехугольники, каждая сторона которых имеет одинаковую длину, все четыре угла являются прямыми углами.
Периметр квадрата равен сумме длин всех сторон. Таким образом, периметр квадрата можно определить сложением \(4\) сторон.
Периметр определенного квадрата равен \(a + a + a + a\). Поскольку все стороны квадрата одинаковы, вам нужна только одна сторона для определения периметра.
Периметр данного квадрата:
\(a + a + a + a = 4a\) единиц.
Итак, формула нахождения периметра квадрата \(= 4 ×\) (длина любой \(1\) стороны).
Площадь квадрата равна произведению длины каждой стороны на себя. Итак, \(Площадь = a×a\) , где \(a\) — длина каждой из сторон квадрата.
Часто вы будете много раз находить текстовые задачи, где представлены \(2\) значений в \(1\) этих формул, и вы должны найти \(3\)rd.
Площадь и периметр – Пример 1:
Вычислите площадь прямоугольника \(10\) см в длину и \(5\) см в ширину.
Решение:
Площадь прямоугольника находится по формуле \(A=длина × ширина\). Тогда площадь прямоугольника: \( 10 × 5=50\)
Площадь и периметр – Пример 2:
Сара планирует украсить скатерть лентой. Если эта скатерть квадратная и каждая сторона квадрата равна \(3\) метрам. Сколько лент ей нужно, чтобы украсить эту скатерть?
Решение:
Вы знаете, что площадь квадрата равна: \(a+a+a+a=4a\). Тогда количество ленты, которое нужно Саре, равно: \( 4 × 3=12\) метров
Упражнения для площади и периметра
Мазь .
- Площадь прямоугольника равна \(30\) квадратных метров. Если ширина этого прямоугольника \(5\) метров, какова его длина?
- Какова площадь квадрата со стороной \(8\) см?
- Найдите периметр прямоугольника, длина которого \(7\) см, а ширина \(3\) см.
- Каков периметр квадратного сада со стороной \(10\) метров?
Ответы
- \(\color{blue}{6}\)
- \(\color{blue}{64}\)
- \(\color{blue}{20}\)
- \ (\color{blue}{40}\)
Что такое площадь и периметр? Определение, формула, примеры, факты
Периметр двумерной фигуры – это общее расстояние вокруг соответствующей фигуры.
Для фигур с прямыми сторонами, таких как треугольник, прямоугольник, квадрат или многоугольник; периметр это сумма длин всех сторон.
Площадь двумерной фигуры — это пространство, ограниченное периметром данной фигуры. Чтобы вычислить площадь различных фигур, используйте разные формулы, основанные на количестве сторон и других характеристиках, таких как углы между сторонами.
Если все измерения выражены в сантиметрах, единицы измерения периметра и площади различных форм будут следующими:
Понятия площади и периметра являются основой для понимания евклидовой геометрии и расчета объема объемных фигур в трехмерном пространстве. пространство, такое как конусы, призма, сфера и цилиндр. Кроме того, мы используем эти формулы для вычисления площади и периметра четырехугольников и многоугольников, состоящих из сторон и кривых. Реальная полезность этой концепции в нескольких областях, таких как картографирование, архитектура и геодезия. Геометрическое представление фигур делается путем зарисовки расстояний и площадей для ясности понимания.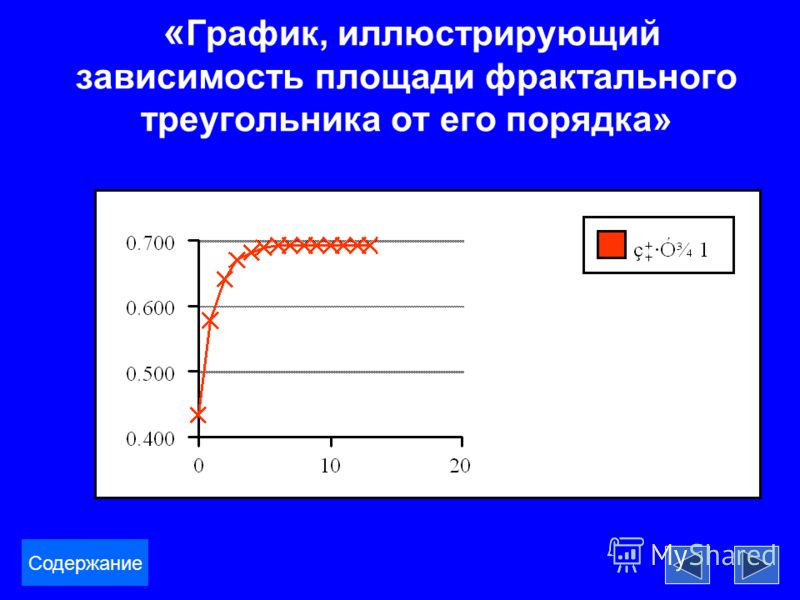
Трехмерные объекты, полученные из двухмерных форм и топографической съемки полей.
1 Площадь треугольника с основанием в 7 единиц равна 21 квадратной единице. Какова высота треугольника?2 единицы 3 единицы 4 единицы 6 единиц Правильный ответ: 6 единиц 2 Какова площадь треугольника с основанием 6 единиц и высотой 10 единиц?16 квадратных единиц 30 квадратных единиц 32 квадратных единиц 60 квадратных единиц Правильный ответ: 30 квадратных единиц 3 Если площадь квадрата 36 кв.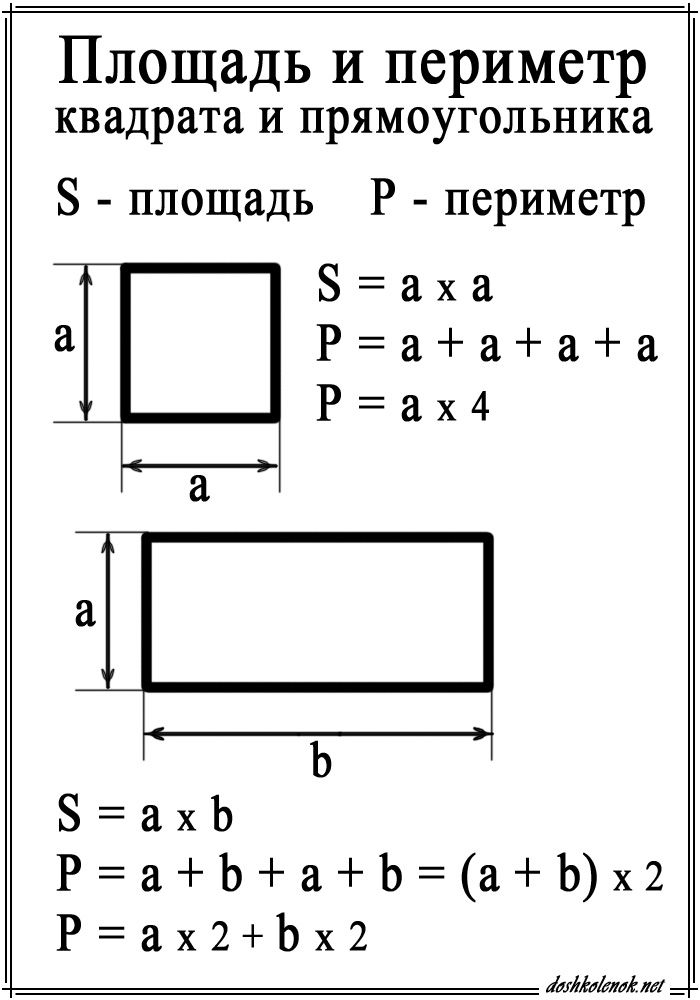 см. Каков его периметр?9 см 12 см 18 см 24 см Правильный ответ: 24 см 4 Чему равен периметр правильного пятиугольника со стороной 8 см?32 см 40 см 64 см 80 см Правильный ответ: 40 см |
Как объяснить ребенку разницу между площадью и периметром?
Во-первых, площадь фигуры — это поверхность или плоское пространство, которое покрывает фигура, тогда как периметр фигуры представляет собой расстояние вокруг ее границы. Во-вторых, площадь измеряется в квадратных единицах, тогда как периметр измеряется в линейных единицах.