Камень ножницы бумага цу е фа что это значит: Вопрос дня: Что значит «цу-е-фа» в игре «камень-ножницы-бумага»?

«Камень-ножницы-бумага» и теория игр / Хабр

Игра «камень-ножницы-бумага» отлично подходит для того, чтобы решить, кому придётся выносить мусор. Но замечали ли вы, что происходит, когда вместо трёх выбрасываний игра продолжается раунд за раундом? Сначала вы выбираете принцип, который даёт вам преимущество, но потом противник быстро понимает его и обращает в свою пользу. В процессе изменения стратегий вы постепенно достигаете точки, в которой ни одна из сторон не может дальше совершенствоваться. Почему же такое происходит?

В 1950-х математик Джон Нэш доказал, что в любом виде игры с конечным количеством игроков и конечным количеством вариантов (таком, как «камень-ножницы-бумага») всегда существует смешение стратегий, при которой ни один игрок не может показать результатов лучше изменением только собственной стратегии. Теория таких устойчивых наборов стратегий, которые называются “равновесиями Нэша”, совершила революцию в области теории игр, изменила направление развития экономики и способы изучения и анализа всего — от политических договоров до сетевого трафика.

А ещё она позволила Нэшу получить в 1994 году Нобелевскую премию.

Так как же выглядит равновесие Нэша в игре «камень-ножницы-бумага»? Давайте смоделируем ситуацию, в которой есть вы (Игрок A) и ваш противник (Игрок B), снова и снова играющие в игру. В каждом раунде победитель получает очко, проигравший теряет очко, а ничья засчитывается как ноль очков.

Предположим, Игрок B выбрал (глупую) стратегию выбора в каждом раунде бумаги. Через несколько раундов побед, проигрышей и ничьих вы скорее всего заметите его систему и выработаете выигрышную контрстратегию, выбирая в каждом раунде ножницы. Давайте назовём этот набор стратегий (ножницы, бумага). Если в результате каждого раунда получаются ножницы против бумаги, то вы проложите себе дорогу к идеальной победе.

Но Игрок B вскоре замечает недальновидность этого набора стратегий. Увидев, что вы выбираете ножницы, он переключается на стратегию постоянного выбора камня. Этот набор стратегий (ножницы, камень) начинает выигрывать для Игрока B.

Но, разумеется, теперь вы перейдёте к бумаге. На протяжении этих этапов игры Игроки A и B используют то, что называется «чистыми» стратегиями — единственные стратегии, выбираемые и реализуемые постоянно.

Очевидно, здесь нельзя достичь равновесия: для каждой чистой стратегии, например «всегда выбирать камень», можно выработать контрстратегию, например «всегда выбирать бумагу», которая заставит изменить стратегию ещё раз. Вы и ваш противник постоянно будете преследовать друг друга в круге стратегий.

Но вы также можете попробовать «смешанную» стратегию. Предположим, что вместо выбора одной стратегии вы можете в каждом раунде случайным образом выбирать одну из чистых стратегий. Вместо «всегда выбирать камень» смешанная стратегия может иметь вид «в половине случаев выбирать камень, в другой половине выбирать ножницы». Нэш доказал, что когда допустимы такие смешанные стратегии, в каждой подобной игре должна быть по крайней мере одна точка равновесия. Давайте её найдём.

Какова же разумная смешанная стратегия для «камня-ножниц-бумаги»? Интуитивно кажется разумным, что это «выбирать камень, бумагу или ножницы с равной вероятностью». Такая стратегия записывается как . Это означает, что камень, ножницы и бумага выбираются с вероятностью . Является ли эта стратегия хорошей?

Предположим, что стратегия вашего противника имеет вид «всегда выбирать камень». Это чистая стратегия, которую можно обозначить как . Какими будут результаты игры при наборе стратегий для Игрока A и для Игрока B?

Чтобы получить более чёткую картину игры, мы построим таблицу, в которой будут показаны вероятности каждого из девяти возможных результатов каждого раунда: камень у A, камень у B; камень у A, бумага у B; и так далее. В приведённой ниже таблице верхняя строка обозначает выбор Игрока B, а левый столбец — выбор Игрока A.

A | B	К	Б	Н
К		0	0
Б		0	0
Н		0	0

Каждый элемент таблицы обозначает вероятность пары выбранных вариантов для каждого раунда. Это просто произведение вероятностей того, что каждый из игроков сделает соответствующий выбор. Например, вероятность того, что Игрок A выберет бумагу, равна , а вероятность того, что Игрок B выберет камень, равна 1, то есть вероятность (камень у A, камень у B) равна . Но вероятность (бумага у A, ножницы у B) равна , поскольку вероятность выбора Игроком B ножниц равна нулю.

Как же проявит себя Игрок A при своём наборе стратегий? Игрок A выиграет одну треть времени (бумага, камень), проиграет в одну треть времени (ножницы, камень) и в одну треть времени сыграет вничью (камень, камень). Мы можем вычислить количество очков, которые в среднем получит Игрок A в каждом раунде, вычислив сумму произведения каждого результата на соответствующую вероятность:

Таким образом, в среднем Игрок A будет получать по 0 очков за раунд. Вы будете выигрывать, проигрывать и играть вничью с одинаковой вероятностью. В среднем, количество побед и поражений уравновесят друг друга, и по сути, оба игрока придут к ничьей.

Но как мы уже говорили, вы можете улучшить свои результаты, изменив свою стратегию, предполагая, что противник не будет менять свою стратегию. Если вы перейдёте к стратегии (0,1,0) («каждый раз выбирать бумагу»), то таблица вероятностей будет выглядеть так:

A | B	К	Б	Н
К	0	1	0
Б	0	0	0
Н	0	0	0

В каждом раунде вы будете заворачивать в свою бумагу камень противника и получать за каждый раунд по одному очку.

То есть эта пара стратегий — для A и для B — не является равновесием Нэша: вы, как Игрок A, можете улучшить свои результаты, изменив стратегию.

Как мы увидели, чистые стратегии, похоже, не ведут к равновесию. Но что, если ваш противник попробует использовать смешанную стратегию, например ? Это стратегия «в половине случаев выбираем камень; бумаге и ножницам достаётся по четверти случаев».

Вот, как будет выглядеть таблица вероятностей:

A | B	К	Б	Н
К
Б
Н

А вот таблица «вознаграждений» с точки зрения Игрока A; это количество очков, получаемых Игроком A в каждом из результатов.

A | B	К	Б	Н
К	0	-1	1
Б	1	0	-1
Н	-1	1	0

С помощью умножения мы объединим две таблицы, чтобы вычислить среднее количество очков, получаемых Игроком A за каждый раунд.

В среднем Игрок A снова за раунд зарабатывает 0 очков. Как и раньше, этот набор стратегий, для A и для B, в результате приводит к ничьей.

Но как и раньше, вы, как Игрок A, можете улучшить свои результаты, сменив стратегию: против стратегии Игрока B , Игрок A должен выбрать . Вот таблица вероятностей:

A | B	К	Б	Н
К
Б
Н

а вот итоговый результат для A:

То есть этот набор стратегий — для A и для B — даёт в среднем Игроку A по очка за раунд. После 100 игр Игрок A будет впереди на 6,25 очка. У Игрока A есть большой стимул к изменению стратегии. То есть набор стратегий для A и для B тоже не является равновесием Нэша.

Но теперь давайте рассмотрим пару стратегий для A и для B. Вот соответствующая таблица вероятностей:

A | B	К	Б	Н
К
Б
Н

Благодаря симметрии мы можем быстро вычислить общий результат:

И снова вы и ваш противник пришли к ничьей. Но разница здесь в том, что никакой из игроков не имеет стимула к изменению стратегий! Если Игрок B перешёл бы к любой неуравновешенной стратегии, где один вариант выбора — допустим, камень — выбирался чаще других, то Игрок A просто бы изменил свою стратегию и стал чаще выбирать бумагу. В конце концов это привело бы к положительному общему результату Игрока A в каждом раунде. Именно это и происходит, когда Игрок A выбирает стратегию против стратегии Игрока B .

Разумеется, если Игрок A перейдёт от к неуравновешенной стратегии, Игрок B аналогичным образом сможет получить преимущество. Поэтому ни один из игроков не может улучшить свои результаты только за счёт изменения собственной стратегии. Игра достигла равновесия Нэша.

Доказанный Нэшем факт, что такие игры имеют подобные равновесия, очень важен по нескольким причинам. Одна из причин заключается в том, что многие ситуации из реальной жизни можно смоделировать в виде игр. Когда группа людей вынуждена выбирать между личной и коллективной выгодой — например, при переговорах или в процессе конкуренции за общие ресурсы — можно увидеть, что используются стратегии и оцениваются выигрыши. Работа Нэша оказала такое большое влияние в том числе и благодаря вездесущей природе этой математической модели.

Другая причина заключается в том, что равновесие Нэша, в некотором смысле, является положительным результатом для всех игроков. При достижении этого равновесия никто из игроков не может улучшить свои результаты, меняя собственную стратегию. Могут существовать коллективные результаты, которых можно достичь, когда все игроки действуют в идеальном сотрудничестве, но если вы можете контролировать только себя, то равновесие Нэша будет наилучшим из результатов, которого вы можете добиться.

Поэтому можно надеяться, что «игры» наподобие экономических пакетов стимулирования, налоговых кодексов, условий договоров и конструкций сетей приведут к равновесиям Нэша, при которых отдельные лица, действующие в собственных интересах, придут к устраивающему всех результату и системы станут стабильными. Но играя в такие игры, разумно ли будет предположить, что игроки естественным образом придут к равновесию Нэша?

Есть искушение думать так. В нашей игре «камень-ножницы-бумага» мы сразу смогли догадаться, что ни один из игроков не смог бы сыграть лучше, кроме как играя совершенно случайно. Но частично так получается потому, что предпочтения всех игроков известны всем остальным игрокам: все знают, сколько каждый другой выиграет и проиграет при каждом из результатов. Но что, если предпочтения более скрыты и сложны?

Представьте новую игру, в которой Игрок B получает три очка, когда он побеждает против ножниц, и одно очко за любую другую победу. Это изменит смешанную стратегию: Игрок B чаще будет выбирать камень, надеясь на тройное вознаграждение при выборе Игроком A ножниц. И хотя разница в очках не влияет непосредственно на вознаграждения Игрока A, получившееся изменение стратегии Игрока B приведёт к новой контрстратегии A.

А если каждое из вознаграждений Игрока B было бы разным и скрытым, то Игроку A потребовалось бы какое-то время на выяснение стратегии Игрока B. Должно пройти много раундов, прежде чем Игрок A догадается, допустим, как часто Игрок B выбирает камень, чтобы понять, как часто ему нужно выбирать бумагу.

Теперь представьте, что в «камень-ножницы-бумагу» играют 100 человек, и у каждого из них есть разный набор тайных вознаграждений, каждое из которых зависит от того, сколько из 99 своих противников они побеждают с помощью камня, ножниц или бумаги. Сколько времени уйдёт на вычисление всего лишь правильной частоты выбора камня, ножниц или бумаги, которая необходима для достижения точки равновесия? Скорее всего, очень много. Возможно, больше, чем будет длиться сама игра. Возможно, дольше, чем срок жизни самой Вселенной!

По меньшей мере, совсем неочевидно, что даже абсолютно рациональные и вдумчивые игроки, выбирающие хорошие стратегии и действующие в собственных интересах, в результате прийдут к равновесию в игре. Эта мысль лежит в основе статьи, опубликованной онлайн в 2016 году. В ней доказывается, что не существует общего решения, которое во всех играх смогло бы привести хотя бы к приближенному равновесию Нэша. Нельзя сказать, что идеальные игроки никогда не стремятся к равновесию в играх — часто они действительно стремятся. Это просто значит, что нет никаких причин полагать, что если в игру играют идеальные игроки, равновесие будет достигнуто.

Когда мы разрабатываем транспортную сеть, мы можем надеяться, что все игроки, то есть водители и пешеходы, каждый из которых стремится найти скорейший путь домой, коллективно достигнут равновесия, в котором ничего нельзя выиграть, выбрав другой маршрут. Мы можем надеяться, что невидимая рука Джона Нэша направит их таким образом, что их конкурентные и совместные интересы — выбор кратчайшего возможного маршрута при избежании транспортных пробок — создадут равновесие.

Но наша игра в «камень-ножницы-бумагу» с постоянно увеличивающейся сложностью показывает, что таким надеждам, возможно, не суждено сбыться. Невидимая рука может и управлять некоторыми из таких игр, но другие игры сопротивляются ей, заманивая игроков в ловушку бесконечной конкуренции за выигрыш, который постоянно находится вне пределов досягаемости.

1. Допустим, Игрок B играет со смешанной стратегией . Какую смешанную стратегию должен выбрать A, чтобы максимизировать количество своих выигрышей в длительной перспективе?
2. Допустим, Игрок B играет со смешанной стратегией . Какую смешанную стратегию должен выбрать A, чтобы максимизировать количество своих выигрышей в длительной перспективе?
3. Как может измениться динамика игры, если за ничью каждому из игроков будет даваться очко?

Mazz_O Boardgamer: Детское.

Обзор настольной игры “Камень, ножницы, бумага

Детское. Обзор настольной игры “Камень, ножницы, бумага – ЦУ-Е-ФА!”

Продолжаю вас знакомить с настольными играми от издательства DoJoy. На этот раз выбор пал на игру для двоих участников с прямым взаимодействием. Тенденция издателя делать “салат” из известных механик присутствует, что из этого получилось, читаем в этой заметке.

.
ЧТО ВНУТРИ?

В большой, но неувесистой коробке типа крышка/дно скрывается игровое поле 6х6 клеток и фишки (картонки с подставками) двух команд – отличников и хулиганов. Коробку при таком же наполнении можно было бы уменьшить хотя бы по высоте. А если поле складывалось бы вчетверо, то с размерами можно было поиграть ещё больше.

Две команды,

двоечники

хулиганы и

очкарики

отличники. В каждой команде по 18 персон. За спиной каждого в руках зажат один из знаков всем известной игры, камень, ножницы или бумага. Есть пара уникальных персонажей, с флагом и динамитом. Первый – главная цель для вашего оппонента (напасть и одолеть), второй – сюрприз с бабахом, который взорвёт любого напавшего на него, но и сам взорвётся.

В игровой партии используются лишь по 12 персон с каждой стороны, что даёт простор в построении стратегии в игре (поставить армию с ножницами или использовать смешанную тактику).

КАК ИГРАТЬ?

Игроки выбирают, кто за какую команду играет, и расставляют 12 персонажей на игровое поле “спиной” к себе так, чтобы противник не видел предметов. Обязательно должен стоять персонаж с флагом, ведь найти и одолеть его – главная задача для противника. Запасных не убираем далеко, могут пригодиться.

В свой ход игрок должен сделать всего одно действие: совершить один шаг ортогонально (горизонтально или вертикально) одной из своих фишек.

Когда игрок выбирает походить на клетку, занятую персонажем оппонента, начинается главная часть игры – сравнение предметов за спиной у персонажей.

“Камень, ножницы, бумага – ЦУ-Е-ФА!” Бумага побеждает камень, камень побеждает ножницы, ножницы побеждают бумагу. Проигравший убирается с поля обратно в коробку.

Если победил тот персонаж, чей был ход (читай – нападающий, инициировавший бой), то он встаёт на клетку, где был оппонент. Если побеждает защищавшийся, то он остаётся на месте.

Нередко случаются спорные моменты, когда бой проходит у персонажей с одинаковым предметом. Тогда в спор вступают сами игроки.

Уже на руках происходит классическая битва интуиций и проигравшая сторона убирает своего персонажа с поля.
Важно! Тот предмет, который принёс победу игроку, должен быть установлен на персонажа, участвовавшего в бою. На примере выше игрок должен поставить персонажа с камнем вместо оставшегося на поле персонажа с бумагой.

Когда атакуют персонажа с флагом, игра заканчивается, так как флаг в защите победить не может никого (в атаке он ещё может уложить персонажа противника с флагом). Потерял флаг – проиграл.
Да, не забываем про динамитного персонажа. Сам он ходить не имеет права, но если его атаковать, взрывается и он, и атакующий.

Вот и вся игра.

ВПЕЧАТЛЕНИЯ.
С первого взгляда в игре “Камень, ножницы, бумага – ЦУ-Е-ФА!” любитель настольных игр узнает известнейшую игру “Стратего”. Однако, если бы это был простой клон игры, каких множество, ко мне в блог бы игра не попала. Две игры могут жить дружно на одной полке по нескольким причинам:

• “Стратего” сложней и стратегичней. Там и персонажей больше с разной силой, и сапёры с бомбами… в общем, это следующий этап после игры, о которой я рассказываю. =)
• “ЦУ-Е-ФА” более универсальная по тематике: “Стратего” – явная игра для мужского пола с полководцами, бомбами и прочей военной атрибутикой, тогда как герой нашего обзора – эдакий флешмоб со школьниками, играющими в камень-ножницы-бумагу.  

С “ЦУ-Е-ФА” легко справляется ребёнок 5 лет, проверено. Здесь нет ни букв, ни цифр, а значит, старший курс детского сада справится. Из-за лёгкости усвоения правил и довольно простого и логичного процесса эта игра появляется в моей домашней детской ячейке довольно часто.

Качество исполнения и арт игры достаточны для того, чтобы привлечь внимание ребёнка. Взрослый же реагирует на эту коробку достаточно предсказуемо: “Это что за обманка? С каких это пор надо покупать целую коробку, чтобы поиграть в камень-ножницы-бумагу?” Поэтому мне сложно оценить покупательный потенциал игры вслепую. 

Если говорить о правилах игры, лично мне не хватало нескольких нюансов, назову их домашними правилами:

1) Недвигающийся динамит. Этот момент мгновенно палит, где стоит фишка. Я бы предложил разрешить динамиту двигаться, но запретить нападать. Тогда противника можно будет ввести в заблуждение. 

2) Также я бы предложил каждому персонажу, кто участвовал в бою (читай – показал свой предмет), после боя меняться на другого из запаса. Причём можно менять на такой же предмет, что опять добавляет игре блефа. 

Стратегическую составляющую игры нужно правильно оценить: эта игра на блеф, интуицию и немного на логику. Лозунг “легче шахмат, сложнее шашек” немного нечестен в плане именно стратегичности (шашечники-разрядники – страшная сила). Сложнее в плане нюансов правил? Ну да, немного. Но по зависимости от уровня игроков совсем из другой песни. 

Итого, сегодня я рассказал вам про второй “салат” от издательства DoJoy. Впереди ещё одна игра под названием “Тугрики”, в которой те, кто за 30, легко узнают одну карточную, но подзабытую игру.  Всем хороших выходных!

Подписаться на: Комментарии к сообщению (Atom)

Каменные ножницы для бумаги и бутылка с водой. Камень, ножницы, бумага (Детская стишка, игра)

Камень, ножницы, бумага – детская стишка и игра. Счетная таблица используется для определения кого-либо путем случайного подсчета. Счетчик начинает произносить счетную считалку, указывая на каждое слово на участников игры последовательно по часовой стрелке. Выбранным считается тот, на ком заканчивается рифма (например, он поедет).

Камень, ножницы, бумага также используется как игра. Игроки (обычно 2 игрока) вместе считают стишок вслух, потрясая кулаками. В конце считалки одновременно показывают руками один из трех знаков: камень (кулак), ножницы (два вытянутых пальца) или бумагу (открытая ладонь).

Победитель определяется по следующим правилам:

Камень побеждает ножницы («камень затупляет или ломает ножницы»)

Scissors beat paper («ножницы режут бумагу»)

Бумага бьет камень («бумага оборачивает камень»)

Если игроки показали одинаковый знак, то результат игры ничья.

Существует множество вариантов этого счетчика. Например:

Вариант 1

Камень, ножницы для бумаги,

И бутылка лимонада

И коробку конфет

И отвертку – тоже!

Карандаш, огонь, вода…

Вариант 2

Камень, ножницы, бумага,

Карандаш, огонь, вода,

И бутылка лимонада

И железная рука!

Вариант 3

Камень, ножницы, бумага,

И колодец тоже

“Камень, ножницы, бумага – ТСУ-Э-ФА!” – это довольно забавная игра по мотивам игры нашего детства. Я уже рассказывал об игре “Физзи” от производителя DOJoy. Эта игра не менее динамична и увлекательна.

Цена 1290 рублей

Где купить?

Игра продается во многих крупных интернет-магазинах, в том числе и в моем магазине, где можно применить скидку 25%. DOJoy есть на официальном сайте

Пакет.

Все игры этого производителя покорили меня своими красочными, монументальными коробками.

Что внутри?

Внутри коробки складное игровое поле из плотного картона в клетку и два листа с изображением главных героев. Подставки в отдельном пакете.

Сколько человек может играть?

ТСУ-Э-Фа — игра для двоих. Подойдет даже для романтического вечера. Особенно, если вы очень увлечены. Тогда вы сможете сцепиться в решающей битве, не успев закончить игру.

Или встретиться с бывшими одноклассниками. Во время игры обязательно расскажите собеседнику историю из детства, начав со слов «Ты помнишь…». История должна быть частью вашего совместного детства с вкраплениями ярких и незабываемых моментов. Натянули на косичку? Прищемил палец книгой? Пришло время вспомнить!

Главное в процессе выяснения отношений не задавить цифры.

Весело играть со старыми школьными друзьями. Особенно, если вы их бьете или они бьют вас.

Обучение.

Перед игрой поле должно быть выровнено,

и выдавить фигурки из листов, в которых они закреплены.

Ножницы не нужны.

Можно подключить к процессу детей, так как фигурки выдавливаются легко.

Каждая фигурка должна быть поставлена ​​на подставку. Готовый? Сейчас они стабильны.

Теперь перед вами предстали две банды. Хотя “банда ботаников” звучит как-то странно…

Вторая группа состоит из гоников-хулиганов. Вполне реально представить это забавное противостояние.

Фигурки двухсторонние. Лицевая сторона – это их целеустремленные физиономии, а тыльная, в каждом кулаке крепко сжат какой-то предмет.

Что это может быть?

• камень
• бумага
• ножницы

Как играть?

При столкновениях человечек с более “сильным” предметом остается в игре, а проигравший персонаж удаляется с доски.

Цель игры

Убить всех противников

Задача игроков – захватить флаг противника.

Вы тоже этого не делали 1000 лет? Тогда пора вернуться в детство!

Самые веселые моменты игры – это когда на поле сталкиваются фигуры с одинаковыми предметами. При этом участники игры складываются на пальцах, определяя, кто останется на игровом столе и с каким предметом за спиной.

Камень-ножницы-бумага это:

Правила игры

Игроки громко считают «Камень… Ножницы… Бумага… Раз… Два… Три», потрясая кулаками. На счет «Три» одновременно показывают с помощью руки один из трех знаков: камень, ножницы или бумагу. Знаки показаны на картинке.

Победитель определяется по следующим правилам:

• Камень побеждает ножницы («камень притупляет или ломает ножницы»)
• Scissors beat paper (“ножницы режут бумагу”)

Если игроки показали одинаковый знак, то засчитывается ничья и игра переигрывается.

В классическом варианте в игру играют два человека, однако может играть большее количество участников. При этом ничья засчитывается в ситуации, когда хотя бы один игрок показал «камень», хотя бы один игрок показал «бумагу» и хотя бы один игрок одновременно показал «ножницы».

История

Игра была изобретена в Китае. Согласно Wuzazzu (Wǔzázǔ – пиньинь, 五雜俎 или 五雜組 – китайский), написанному Се Чжаочжи (謝肇淛) во времена поздней династии Мин. Военачальники поздней династии Хань играли в игру под названием шоушилинь (shǒushìlìng, 手勢令), которая признана эквивалентной современной игре «Камень, ножницы, бумага». Шушилин можно перевести как «ручные команды»

Нет упоминаний об использовании игры в Западной Европе до прямого контакта с Азией. Западные писатели конца 19 века называли ее просто азиатской игрой.

Региональные разновидности

В некоторых регионах эту игру называют «Бу-Це-Фа»: соответственно при игре вместо «раз…два…три…» говорят «бу… це… фа…”. В некоторых регионах также говорят “цу… э… фа…” или “чи… чи… ко…” вместо “раз… два… три.. .”.

В некоторых странах игра называется “Муравей – Человек – Слон”: слон давит человека, человек давит муравья, муравей кусает слона.

В некоторых регионах России существует версия игры, включающая колодец. Он изображен камнем, только пальцы не сжаты плотно, образуя таким образом «колодец».

Счет идет так:

Камень, Ножницы, Бумага,
И колодец
Раз, два, три!

Правила просты – бумага бьет колодец (покрывает), а колодец бьет камень и ножницы (они тонут).

В некоторых регионах России существует усложненная версия этой игры, которая обычно не служит методом выбора человека, а сама по себе является игрой. Помимо «камня», «ножниц» и «бумаги» в этой игре есть «шоколад», «лимонад», «отвертка», «карандаш», «огонь» и «вода».

Правила этой версии игры более сложные:

• Chocolate beats paper («коробка шоколада давит бумагу»)
• Бумага бьет камень («бумага оборачивает камень»)
• Камень побеждает ножницы (“камень ломает ножницы”)
• Ножницы бьют лимонад («ножницы протыкают бутылку лимонада»)
• Лимонад бьет отвертку («отвертка ржавеет в лимонаде»)
• Отвертка побеждает огонь («отвертка не горит в огне»)
• Огонь побеждает шоколад («огонь тает шоколад»)

Вода — самый выгодный и в то же время самый рискованный ход:

• Вода побеждает шоколад, бумагу, отвертку и огонь
• Ножницы, камень, лимонад и карандаш для нанесения воды

Счёт (вступление) для этой версии игры звучит так:

Камень, Ножницы, Бумага,
И бутылка лимонада
И коробка конфет
И отвёртка – тоже!
Карандаш, огонь, вода. ..
Цу-и-фа!

Камень, ножницы, бумага,
Карандаш, огонь, вода,
И бутылка лимонада
И железная рука!
Цу-Э-Фа!

В этом случае железная рука заменяет отвертку, а шоколад полностью исключается (огонь побеждает бумагу)

В эту версию игры удобнее играть при количестве игроков от пяти и более (иначе придется переигрывать много раз).

Отсылки в артах

Герои американского комедийного сериала «Теория большого взрыва» играют в усложненную версию этой игры – «Камень, ножницы, бумага, ящерица, Спок». Правила игры описаны следующим образом:

Ножницы режут бумагу. Бумага оборачивает камень. Камень раздавливает ящерицу, и ящерица отравляет Спока. в то время как Спок ломает ножницы, которые, в свою очередь, отрезают голову ящерице, которая ест бумагу, содержащую улики против Спока. Спок испаряет камень, а камень, конечно же, притупляет ножницы.

Разное

Игра часто упоминается в качестве примера, чтобы проиллюстрировать отсутствие математического свойства транзитивности.

Несмотря на то, что исход игры кажется случайным, при определенных навыках исход игры можно предсказать. После нескольких партий можно распознать некие неслучайные «шаблоны» в поведении соперника. Это связано еще и с тем, что во время второго раунда человек подсознательно показывает то, что могло победить его в прошлом. Так что если в первый раз противник выбросил «камень», то во второй раз желательно показать «ножницы»: он, скорее всего, выберет «бумагу».

По игре проходят чемпионаты мира со значительным призовым фондом, которые освещаются ведущими изданиями. Есть международная федерация и официальные правила соревнований.

Примечания

Ссылки

Фонд Викимедиа. 2010 .

Смотреть что такое “Камень-ножницы-бумага” в других словарях:

Камень, ножницы-бумага – Эту страницу предлагается объединить с Камень, ножницы-бумага, ящерица, Спок… Википедия

Ножницы-бумага Камень – Жесты, используемые в игре (слева направо: камень, ножницы, бумага). Каждый из знаков побеждает один из двух других. Камень, ножницы, бумага – популярная детская ручная игра, известная во многих странах мира. Иногда употребляешь … Википедия

Камень, ножницы, бумага, ящерица, Спок – Эту страницу предлагается объединить с Камень, ножницы, бумага. Объяснение причин и обсуждение на странице Википедии: О… Википедия

Легализация – Эта статья или раздел нуждается в доработке. Просьба улучшить статью в соответствии с правилами написания статей… Википедия

Гейша – Две гейши развлекают клиентов игрой на сямисэне… Википедия

Путь воина (игра) – У этого термина есть и другие значения, см. Путь Воина. Путь воина Разработчик Павел Яковлев Дата выхода 19 января, 2002 Версия Жанр выпуска… Википедия

Камень, ножницы, бумага и телепатия

Поезда дважды упоминались в моей прошлой колонке про пальчиковые игры. И неудивительно — ведь именно в дороге нужны развлечения с минимальным реквизитом. А вот пальчиковый театр, о котором упоминалось в прошлый раз, — для самых маленьких, для двухлеток. А вот четырехлетнему, то есть почти взрослому, интересны более серьезные мальчишеские игры. Не только смотреть и показывать, но и выигрывать!

Когда старшему было четыре года, мы начали коротать время в поездке на метро, ​​играя в «камень, ножницы, бумага». Ну а так как троечки со временем надоедают, мы стали искать варианты посложнее.

Впрочем, начнем с классики. Считается, что игра «камень, ножницы, бумага» (КНБ) была придумана в Древнем Китае, еще во времена династии Мин. Однако цифры там должны были быть другими, и мы ничего об этом не знаем. Наша версия выглядит так. На счет «раз-два-три» (или «цу-э-фа», или «чин-гис-хан») играющие взмахивают руками, а на последнем ударе одновременно выбрасывают одну из фигур на пальцах — или «камень» (все пальцы сжаты в кулак), или «ножницы» (указательный и средний вперед, остальные в кулак), или «бумага» (все пальцы вытянуты вперед, ладонь плоская).

В этом случае каждая фигура побеждает другую – камень затупляет ножницы, ножницы режут бумагу, бумага оборачивает камень. Если выпали одинаковые фигуры – ничья, следующий раунд. Играть можно просто за аккаунт, или например за клики.

Но, как уже было сказано, троечники со временем надоедают. Поэтому, поиграв некоторое время с сыном, я стала запоминать дополнительные — тем более, что в детстве они действительно появлялись в некоторых играх.

Во-первых, иногда добавляли колодец – почти как камень, только с “дыркой”: указательный и большой пальцы образуют букву “о”.

Был еще вариант с колодцем и огнем. Огонь сделан как бумага, только пальцы подняты вверх и растопырены.

Наконец, было очень бредовое предложение “камень, ножницы, бумага, карандаш, огонь, вода и бутылка лимонада”.

Теперь, спустя годы, я понимаю, в чем была главная проблема этих самодельных расширений классического КНБ, и почему эти версии не стали массовыми. Их изобрели люди, которые исходили именно из представления о разнообразии фигур — но не думали о математике. Ведь классический вариант хорош симметрией: каждая фигура выигрывает у одинакового количества конкурентов (одна фигура) и проигрывает столько же конкурентов (одна).

А теперь посмотрите, что произойдет, если мы добавим «хорошо». Этот новый предмет побеждает сразу два других (камень и ножницы). Кроме того, бумага приобретает двойную силу (укрывает колодец и оборачивает камень). При этом камень и ножницы проигрывают: каждый из них бьет только по одной фигуре. Поэтому повысить свои шансы на победу достаточно просто – нужно чаще показывать бумагу и колодец.

Очевидно, что симметрия отношений в данном случае портится четностью фигур. Каждый получает нечетное количество отношений, а это значит, что отношения нельзя разделить поровну на «выигрыши» и «проигрыши».

Попробуем взять пять фигурок, добавив огня. Кстати, довольно часто КНБ использовал не просто счет «раз-два-три», а какую-нибудь поговорку с названием игры. В нашем случае получилось так: «камень, ножницы, бумага, и колодец, и огонь». Поговорка неплохая, цифры тоже понятные. Но каков сейчас баланс сил?

– Камень затупляет ножницы и гасит огонь, но тонет в колодце и заворачивается в бумагу (2 победы, 2 поражения)
– Бумага хорошо оборачивает камень и покрывает, но горит в огне и режется ножницами (2 победы, 2 поражения)
– Огонь плавит ножницы и сжигает бумагу, но гасится колодцем или камнем (2 победы, 2 поражения)
– Колодец топит ножницы и камень и гасит огонь, но накрывается бумагой (3 победы, 1 поражение)
– Ножницы только режут бумагу, проигрывают другим (1 победа, 3 поражения)

Здесь видно четкое искажение ножницами и колодцем. Но это можно легко исправить. Кто сказал, что ножницы должны тонуть в колодце? Наши ножницы будут покруче: они на лету втыкаются в колодец и перерезают его веревку! В общем, ножницы должны хорошо бить — и в этом сценарии игра в пять фигур снова становится симметричной.

Старая добрая игра “Камень-ножницы-бумага”, как мы привыкли думать, построена на чистой удаче (или случайности). Но если бы это было так, то играть в нее было бы не так интересно. Но люди, к сожалению (или к счастью?), на самом деле очень предсказуемые существа. А если знать секрет, то можно управлять не только людьми, но и жизнью.

Каменные ножницы для бумаги!

По словам Грэма Уокера, опытного игрока и организатора 5 чемпионатов мира по этой игре, выиграть можно несколькими способами. Первый — заставить противника не играть определенную фигуру (например, Бумагу) или еще больше повлиять на его выбор — это второй способ. В обоих случаях самое главное — это умение манипулировать так, чтобы ваши оппоненты даже не знали об этом.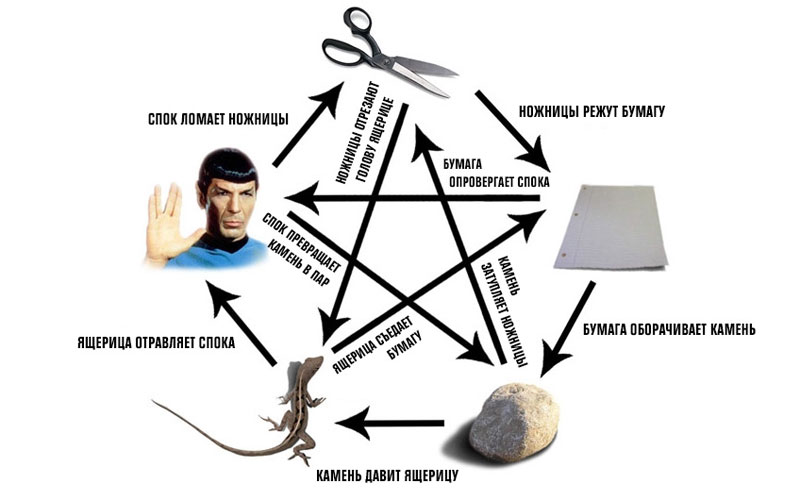

Камень

Эти две стратегии могут быть реализованы посредством выполнения определенных движений, начиная с открытия одной. Опытные игроки говорят, что новички склонны показывать «Рок». Уокер предполагает, что это потому, что психологически они хотят казаться сильнее в глазах врага. Помните, что «Камни — для новичков», и если вы играете с новичком, вам нужно только показать «Бумагу», чтобы выиграть.

С более опытными игроками этот номер не пройдет – они вряд ли сразу покажут камень. Так что, возможно, вам стоит показать ножницы. Такой ход либо побьет «Бумагу», либо будет ничья с «Ножницами».

двойная беда

Если ваш оппонент повторил один и тот же жест два раза подряд, вряд ли он повторит его в третий раз. Люди не любят быть предсказуемыми.

Ваш оппонент дважды подряд показал ножницы? Так что исключаем этот жест и следующим будет либо «Камень», либо «Бумага». В этом случае вам лучше кинуть “Бумагу” – либо вы обыграете “Камень” и выиграете, либо будет ничья.

Уловки разума

Вы можете влиять на разум противника во время простого обсуждения игры перед ее началом. Старайтесь повторять нужные вам жесты во время жестикулирования при разговоре. Подсознание человека очень восприимчиво к мимике и жестам, поэтому ваш собеседник будет реагировать на ваши жесты, даже не подозревая об этом.

Этот трюк может сработать из-за склонности людей подражать себе подобным. Исследования реакции игроков во время последнего чемпионата «Камень-ножницы-бумага» в 2011 году показали, что игроки чаще всего имитировали последний ход соперника.

Таким образом, если перед началом игры показать сопернику жест, то он сработает, но только один раз. Если вы скажете, что собираетесь показывать «Бумагу», ваш оппонент подумает, что вы сказали это намеренно, и не будет показывать этот жест. Это значит, что он точно не выберет «Ножницы» (которые лучше «Бумаги»), а выберет либо «Камень», либо «Бумагу». В итоге, если вы сдержите свое обещание, то либо выиграете, либо снова будет ничья.

Вот и получается, что эта детская игра не так проста, как кажется на первый взгляд. Особенно, когда в нее играют взрослые. Думаю, профессор Лайтман был бы в восторге от такого разнообразия экспериментальных образцов для изучения мимики и жестов человека 😉

Камень-ножницы-бумага | PGpedia

Как играть в «Камень-ножницы-бумага»

«Камень-ножницы-бумага» — игра, в которую играют для разрешения споров между двумя людьми. Считается, что это азартная игра, зависящая от случайной удачи, похожей на подбрасывание монеты или вытягивание соломинки, этой игре часто учат детей, чтобы помочь им урегулировать споры между собой самостоятельно без вмешательства взрослых. Однако на самом деле игра может быть игрой, в которой есть элемент мастерства, требующий быстрого мышления и проницательных рассуждений.1

Игра ведется тремя возможными жестами рук, которые представляют собой камень, ножницы и бумагу. Скала — это сжатый кулак; бумага представляет собой плоскую руку с вытянутыми пальцами и большим пальцем, ладонью вниз; а ножницы – это кулак с полностью вытянутыми указательным и средним пальцами в сторону противостоящего игрока. Камень побеждает ножницы; бумага побеждает камень; и ножницы побеждают бумагу. Если оба игрока подают одинаковый сигнал рукой, это считается ничьей, и игра возобновляется до тех пор, пока не будет определен явный победитель.

Сигналы руками подаются обоими игроками одновременно. Ритуал, используемый для синхронизации игроков друг с другом, чтобы они могли выполнять свои броски одновременно, называется праймом. Это действие требует отведения кулака игрока от полного разгибания руки к плечу, а затем обратно до полного разгибания. Чтобы обеспечить честный матч, игроки должны быть синхронизированы со своими праймами. Перед игрой игроки должны определить, сколько раз они качают руками в основной фазе, обычно два или три раза перед окончательным выполнением броска.2

Вариации игр с мигающими пальцами со всего мира

Игры с мигающими пальцами известны с древних времен, однако происхождение игры остается неясным. Самое раннее известное упоминание найдено на настенной росписи в гробнице на месте захоронения Бени Хасан в Египте, датируемой примерно 2000 годом до нашей эры. Спустя столетия на японском свитке была также найдена игра. Версии игры встречаются в культурах по всему миру. Он по-прежнему очень популярен в Японии, где его называют джан-кен или джанкенпон.3

В Северной Америке игру также называли Rochambeau или Roshambo. Многие пытались приписать это название игре генералу французской армии графу де Рошамбо, который сражался с генералом Джорджем Вашингтоном во время американской революции. Однако глубокие исследования не позволили установить какую-либо связь с общим названием и названием игры.

Хотя до начала 20 века игра не упоминалась в Америке, в биографии упоминалась похожая игра под названием Odds and Evens, Жизнь Сэмюэля Джонсона , в конце 18-го века в Англии, и, скорее всего, он был завезен в Америку по мере того, как иммиграция распространялась в Новый Свет. «четные», а затем оба сжимают кулаки, одновременно считая до трех, и раскрывают одну руку, вытягивая один или несколько пальцев. Комбинация количества вытянутых пальцев на руках обоих игроков определяет победителя: если нечетное число, побеждает игрок, объявивший «шансы»; если четное число, то выигрывает «четный» игрок. 5

Самое раннее упоминание о вариациях игры «Камень-ножницы-бумага» в Америке встречается в сборнике детских игр в Справочнике для руководителей развлекательных заведений , написанном Эллой Гарднер, которая была специалистом по развлечениям в Детском бюро в Вашингтоне, округ Колумбия, опубликовано в 1935 году. Вскоре в других публикациях конца 1930-х годов появились другие ссылки. Популярность игры резко возросла после Второй мировой войны благодаря статьям в армейской газете Stars and Stripes , написанным армейскими репортерами, находившимися в Японии во время оккупации страны США. Явно незнакомые с игрой, репортеры описали игру как версию Odds and Evens. С этого времени игра стала часто упоминаться в книгах, журналах и газетах и ​​прочно вошла в американскую культуру6 9.0005

Игра «Камень-ножницы-бумага» стала отличным помощником на детских площадках. Playworks, организация, которая работает с учащимися в своих школах, знакомит детей с играми на переменах и дает им возможность проводить свои собственные игры и быстро разрешать любые споры с помощью игры «камень-ножницы-бумага». Их успех в разрешении конфликтов достигается благодаря тому, что дети быстро усваивают, что «ладить веселее, чем драться».7

Игра «Камень-ножницы-бумага» стала популярной не только среди детей, но и среди взрослых, которые соревнуются в чемпионатах за крупные денежные призы. У некоторых соревнований были крупные корпоративные спонсоры, и их транслировали по телевидению. В 19В 95 году два брата, Дуг и Грэм Уокер, запустили веб-сайт, посвященный «Камню-ножницам-бумаге». Веб-сайт, получивший название World Rock Paper Scissors Society, должен был стать причудливой данью любимой игре, но его веб-сайт быстро набрал подписчиков, и в 2002 году они организовали свой первый чемпионат с сотнями игроков.8

Когда играют дети в игре их выбор случайный и обычно не просчитывается. Однако, когда играют взрослые, игроки склонны рассуждать о том, как будет играть их противник, что делает игру более похожей на мысленную игру в покер или шахматы. Хорошие игроки используют стратегии, чтобы читать язык тела своих противников, а также блефовать, заставляя их думать, что они знают, какой сигнал рукой они подадут. Часто хорошие игроки заранее определяют свои первоначальные броски и могут планировать серию «гамбитов», которые представляют собой серии бросков типа «камень-камень-камень» или «камень-бумага-бумага»9.

Хорошие игроки осознают, что любители склонны придерживаться определенных паттернов в своей игре. Мужчины, как правило, бросают камень для первого броска, а женщины часто бросают ножницы. Любители обычно не повторяют один и тот же бросок более двух раз подряд, полагая, что это не покажется случайным. Если игрок проигрывает, он с большей вероятностью переключится на другой бросок в следующий раз, а некоторые бессознательно будут бросать любой сигнал рукой, превосходящий их последний бросок. Тщательные наблюдения и стратегии делают игру «Камень-ножницы-бумага» скорее игрой на ловкость, чем просто случайной игрой.10

• 1. Карлайл, Родни П. Редактор. Энциклопедия игры в современном обществе. Лос-Анджелес, Калифорния: SAGE Publications, Inc., 2009. с. 603.
• 2. «Основы игры: как играть — быстрый старт».