Установка рамки и номерного знака
Большинство автовладельцев привыкли к тому, что номерные рамки просто есть. О том, что ее необходимо как-то крепить на авто или снимать и заменять на новую вспоминают обычно, только когда возникает такая необходимость. С проблемой могут столкнуться те, кто:
- приобрел подержанное авто;
- повредил рамку в результате столкновения;
- долго пользовался машиной, и рамка просто пришла в негодность от времени;
- желает поставить новую рамку для номера индивидуального дизайна.
С вышеописанными ситуациями однажды может столкнуться каждый. Поэтому знания, как установить номерную рамку и номер, точно не будут лишними для автовладельцев.
Где должен располагаться номер?В целом крепление рамки номерного знака достаточно простая процедура и не имеет принципиальных различий для разных моделей автомобилей. Главное, чтобы место установки соответствовало требованиям ПДД. В противном случае штраф вам обеспечен. Спереди и сзади авто рамки для номерных знаков необходимо устанавливать так, чтобы они располагались на продольной оси симметрии автомобиля. То есть были строго по центру.
Спереди и сзади авто рамки для номерных знаков необходимо устанавливать так, чтобы они располагались на продольной оси симметрии автомобиля. То есть были строго по центру.
Нередко производитель наносит на бампер отметки, облегчающие установку. Но если их нет, воспользуйтесь рулеткой. Если установить авторамку строго по центру не удается (например, из-за конструктивных особенностей авто), то допускается ее монтаж слева от оси симметрии по направлению движения. Главное, чтобы конструкция не загораживала осветительные приборы, а месторасположение было таким, чтобы номерной знак легко читался с разных ракурсов.
Как закрепить номерную рамку?Сама рамка может быть закреплена на бампере автомобиля при помощи саморезов, болтов или заклепок. Помните, что вам может понадобиться дрель, чтобы высверлить отверстия под рамку на бампере автомобиля.
В самой рамке ничего сверлить не надо. Уже при изготовлении рамок для номеров производители предусматривают в них множество эксцентрических отверстий, что позволяет закрепить элемент на кузове авто практически в любом положении. Форма отверстий под крепления позволяет сдвигать элемент, если вы ошиблись при разметке или если размеры номерной рамки выступают за габариты авто.
Форма отверстий под крепления позволяет сдвигать элемент, если вы ошиблись при разметке или если размеры номерной рамки выступают за габариты авто.
Установка номерного знака в рамку осуществляется по-разному – в зависимости от типа последней. Номер может защелкиваться или просто вставляться в рамку. Важно не использовать для крепления номера прозрачные и светоотражающие элементы – это запрещено правилами. Также нельзя гнуть сам номерной знак, как-то еще менять его геометрию, делать в нем дополнительные отверстия, помимо конструктивно предусмотренных.
Рамки на авто на заказКомпания «АЕР» предлагает большой выбор авторамок собственного производства, которые можно приобрести только оптом, а также заказать изготовление авторамок на заказ – по размеру и дизайну заказчика. Купить номерные рамки в Санкт-Петербурге и других городах России в розницу можно в торговых сетях-партнерах:
- Максидом;
- Лента;
- Ашан;
- Магнит;
- Metro;
Для получения более подробной информации и заказа продукции свяжитесь с нами по телефону +7 (812) 320-07-34.
Как вставить рамку в документ – Эврика
Как вставить рамку в документ?
При оформлении курсовых и дипломных работ в технических и строительных учебных заведениях возникает необходимость вставки рамки на первую и последующие страницы вордовского документа.
В соответствии с ГОСТом различаются рамки для первого листа и последующих листов. На первом листе в рамке штамп большой, на всех последующих – малый.
По нашему опыту большинство студентов вставляют рамку в виде рисунка, при этом рамку необходимо вставить на каждую страницу отдельно и требуется ее каждый раз двигать, так как отступ от края листа получается разным.
Мы используем вставку рамки в виде колонтитула. Это позволяет вставить рамку только на одну любую страницу и она автоматически появиться на всех страницах документа. При этом можно использовать автоматическую нумерацию страниц, а децимальный номер и другие элементы штампа можно набрать только один раз и они появиться на всех страницах одновременно.
Последовательность действий
- Отрыть рабочий документ.
- Если в рабочем документе есть номера страниц их следует удалить.
- Установить размер правого поля в документе 1 см., для того чтобы при автоматической нумерации страниц номер страницы попал в соответствующее поле штампа.
- Открыть документ с рамкой перейти в верхний колонтитул кликнув мышкой в поле колонтитула или на ленте Вставка / Верхний колонтитул / Изменить верхний колонтитул.
- Выделить рамку и скопировать в буфер обмена (Ctrl + С) затем перейти в рабочий документ и вставить рамку (Ctrl + V ). Рамка появиться на всех страницах рабочего документа.
- Проверить расстояние текста от рамки. По ГОСТУ оно должно быть слева не менее 3 мм, внизу и вверху не менее 1 см, если текст внизу страницы налазит на рамку перенесите несколько строк установив курсор в начале строки и выбрать на ленте Вставка / Разрыв страницы
Если требуется вставить на первый лист документа рамки с большим штампом следует:
- Вставить в конце первой страницы разрыв раздела, чтобы колонтитулы первого листа на повторяли колонтитулы последующих Разметка страницы / Разрывы / Разрывы разделов.
 Следующая страница.
Следующая страница. - Перейти в Конструктор колонтитулов. Кликнув на ленте Вставка / Верхний колонтитул / Изменить верхний колонтитул/ Конструктор.
- В Конструкторе колонтитулов отжать кнопку Как в предыдущем разделе.
- Поставить галочку в пункте Особый колонтитул для первой страницы.
- Открыть файл с большим штампом. Выделить рамку, скопировать ее и вставить в рабочий документ.
Вставка номеров страниц.
Для страницы с большим штампом вставить номер страницы вручную.
Для последующих страниц.
- Установить начальный номер страницы Вставка / Номер страницы / Формат номеров страниц.
- Перейти в нижний колонтитул. Кликнуть точно в поле где должен располагается номер страницы.
- Вставить номера страниц. (Вставка / Номер страницы / Текущее положение / Простой номер ).
Образцы рамок для документов с большим штампом приведены здесь,
а с малым штампом здесь.
Десять кадров | Определение, примеры, подготовка, использование и номера 1-20
Определение Десятичные кадры представляют собой прямоугольные кадры размером два на пять, в которые можно помещать такие объекты, как счетчики, для отображения чисел, меньших или равных десяти. Десять рамок часто используются в качестве инструментов для обучения числам до 10. Другими словами, десятая рамка представляет собой прямоугольник с десятью равными пробелами. Есть пять пробелов сверху и пять пробелов снизу. Ниже показано, как выглядит 10-кадр – 9.0007
Десять рамок часто используются в качестве инструментов для обучения числам до 10. Другими словами, десятая рамка представляет собой прямоугольник с десятью равными пробелами. Есть пять пробелов сверху и пять пробелов снизу. Ниже показано, как выглядит 10-кадр – 9.0007
Чтобы сделать десять рамок, необходимо выполнить следующие шаги –
- Сначала сделайте рамку из десяти равных ячеек. Эти ячейки должны быть размещены в виде прямоугольника, состоящего из пяти ячеек вверху и пяти ячеек внизу.
- Всегда сначала заполняйте верхний ряд, начиная слева. Таким же образом считываются и десять кадров.
- Когда верхний ряд заполнится, обработайте с расположенными внизу фишками заполнения. Здесь снова важно отметить, что нижний ряд также должен быть заполнен слева.
Таким образом, можно использовать стандартный способ для создания десяти фреймов
Использование десяти фреймовДесять фреймов полезны следующим образом –
- 10.

- Десять кадров помогают развить чувство числа.
- Десять рамок полезны для понимания отношений между числами, особенно для чисел от 1 до 10.
- Десять рамок помогают детям визуализировать числа, что облегчает им понимание работы с числами.
- Десять фреймов помогают детям понять, как составлять и разлагать числа.
Десять фреймов находят свое применение в понимании сложения и вычитания чисел до 10. Итак, ниже приведены области, в которых мы можем широко использовать десять фреймов в качестве учебного пособия –
- Подсчет чисел
- Сложение чисел
- Вычитание чисел
Давайте узнаем о них больше.
Счет чисел на десяти рамкахДесять рамок можно эффективно использовать, чтобы помочь ребенку научиться считать числа от 1 до 10.
Давайте сначала перечислим числа от 1 до 10. У нас есть,
Номер Номер Имя
1 ONE
2 два
3 три
4 четыре
5 пять
6 шесть
7 Семь
8 восемь
9 Din
10 Ten
8
10 100007
Теперь давайте разберемся с представлением этих чисел с помощью десяти фреймов.
1 (один)
2 (два)
3 (три)
4 (четыре)
5 (пять)
6 (шесть)
7 (семь)
8 (восемь)
9 (Девять)
10 (Десять)
Десять Рамок для чисел от 1 до 20Давайте сначала разберемся с составом чисел от 1 до 100. Начиная с 1 и увеличивая каждое число на 1, мы можем сформировать числа от 1 10 100, как показано ниже –
| 1 | 10 + 1 = 11 | 20 + 1 = 21 | 30 + 1 = 31 | 40 + 1 = 41 | 50 + 1 = 51 | 60 + 1 = 6110120 | 50 + 1 = 51 | . 70 + 1 = 71 | 80 + 1 = 81 | 9 + 1 = 91 |
| 1 + 1 = 2 | 11 + 1 = 12 | 21 + 1 = 22 | 31 + 1 = 32 | 41 + 1 = 42 | 51 + 1 = 52 | 61 + 1 = 62 | 71 + 1 = 72 | 81 + 1 = 82 | 91 + 1 = 92 | |
| 2 + 1 = 3 | 12 + 1 = 13 | 22 + 1 = 23 | 32 + 1 = 33 | 42 + 1 = 43 | 52 + 1 = 53. | 62 + 1 = 63 | 72 + 1 = 73 | 82 + 1 = 83 | 92 + 1 = 93 | |
| 3 + 1 = 4 | 13 + 1 = 14 | 23 + 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1 = 1. 24 | 33 + 1 = 34 | 43 + 1 = 44 | 53 + 1 = 54 | 63 + 1 = 64 | 73 + 1 = 74 | 83 + 1 = 84 | 93 + 1 = 94 | |
| 4 + 1 = 5 | 14 + 1 = 15 | 24 + 1 = 25 | 34 + 1 = 35 | 44 + 1 = 45 | .54 + 1 = 55 | 64 + 1 = 65 | 74 + 1 = 75 | 84 + 1 = 85 | 94 + 1 = 95 | |
| 5 + 1 = 6 | 15 + 1 = 16 = 16 = 16 = 16 = 16 = 16 = 16. | 25 + 1 = 26 | 35 + 1 = 36 | 45 + 1 = 46 | 55 + 1 = 56 | 65 + 1 = 66 | = 76 + 7 | 85 + 1 = 86 | 95 + 1 = 96 | |
| 6 + 1 = 7 | 16 + 1 = 17 | 26 + 1 = 27 | 36 + 1 = 37 | 46 + 1. 47 47 | 56 + 1 = 57 | 66 + 1 = 67 | 76 + 1 = 77 | 86 + 1 = 87 | 96 + 1 = 97 | |
| 7 + 1 = | ||||||||||
| 7 + 1 = | ||||||||||
| 7 + 1 = | ||||||||||
| 27 + 1 = 28 | 37 + 1 = 38 | 47 + 1 = 48 | 57 + 1 = 58 | 67 + 1 = 68 | 77 + 1 = 78 | 87 + 1 = 88 | 97 + 1 = 98 | |||
| 8 + 1 = | 18 + 1 = 1 | 28 + 1 = 29 | 38 + 1 = 39. | 48 + 1 = 49 | 58 + 1 = 59 | 68 + 1 = 69 | 78 + 1 = 79 | 88 + 1 = 89 | 98 + 1 = 99 | |
| 98 + 1 = 99 | 98 + 1 = 99 | 98 + 1 = 99 | 98 + 1 = 99 | 098 + 1 = 99 | . 1019 + 1 = 20 | 29 + 1 = 30 | 39 + 1 = 40 | 49 + 1 = 50 | 59 + 1 = 60 | 69 + 1 = 70 | 79 + 1 = 80 | 89 + 1 = 90 | 99 + 1 = 100 |
Приведенная выше таблица ясно демонстрирует следующее –
Число может быть записано как 10 + 0 = 1 0
Число 11 может быть записано как 10 + 1 = 1 1
Число 12 может быть записано как 10 + 2 = 1 2
Число 13 можно записать как 10 + 3 = 1 3
Число 14 можно записать как 10 + 4 = 1 4
Число 15 можно записать как 10 + 5 = 1 5
Число 16 можно записать как 10 + 6 = 1 6
Число 17 можно записать как 10 + 7 = 1 7
число 18 можно записать как 10 + 8 = 1 8
число 19 можно записать как 10 + 9 = 1 9
число 20 можно записать как 10 + 10 = 2 0
Аналогичным образом мы можем записать любое число, используя десять кадров.
Сложение в математике может быть определено как процесс объединения двух или более чисел вместе для получения нового итога или суммы.
Мы знаем, что однозначными числами являются 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Это порядок, в котором мы считаем числа, где 2 идет после 1, 3 идет после 2 и так далее . Однозначное число имеет разрядное значение единицы в разрядной системе чисел.
Существуют различные методы, помогающие детям понять, как складывать числа. Давайте обсудим эти методы –
- Сложение прямым счетом
- Сложение с использованием десяти кадров
Рассмотрим ситуацию, когда у вас есть 3 шоколадки. Ваш брат дает вам еще 4 шоколадки. Сколько шоколадок у тебя сейчас?
Чтобы добавить 4 шоколадки к 3 шоколадкам, которые у вас уже есть, начиная с 3, вы переместитесь на 4 позиции вправо от подсчета чисел. Итак, 4 балла после 3, в системе счисления это 7. Значит, 3 + 4 = 7
Итак, 4 балла после 3, в системе счисления это 7. Значит, 3 + 4 = 7
Мы можем складывать два или более однозначных числа с помощью десяти фреймов. Возьмем различные однозначные числа и проверим представление их сложения с помощью десяти фреймов –
1 (Один) + 2 (два) = 3 (Три)
2 (Два) + 3 (Три) = 5 (Пять)
3 (три) + 5 (пять) = 8 (восемь)
Сложение однозначного числа с двузначнымПри счете чисел двузначные числа начинаются с 10. Тогда мы имеем 11, 12, 13, 14, 15, … и так далее. Здесь важно отметить, что двузначное число «ab» может быть записано в виде 10 x a + b, где a имеет значение разряда десятков, а b — значение единицы в системе счисления.
Существуют различные методы, помогающие детям понять, как складывать однозначное число с двузначным. Рассмотрим некоторые из этих методов:
- Сложение без переноса вперед
- Сложение с переносом вперед
- Сложение с использованием десяти кадров , цифра в разряде единиц первого числа будет добавлена к цифре в разряде единиц второго числа.

Давайте разберемся на примере.
Предположим, мы хотим сложить 5 и 13.
5 – 5 стоит на месте единицы в числе.
13 – 1 – это разряд десятков, а 3 – разряд единиц.
Итак, мы складываем цифру единицы из обоих чисел, как показано ниже –
Здесь мы видим, что 5 + 3 = 8 < 10, поэтому полученный результат был однозначным числом на месте единицы. А вот если бы мы сложили числа 5+16, то получили бы 5+6=11, то как бы мы написали в ответе 11. Здесь вступает в силу концепция переноса вперед.
Сложение с переносомРассмотрим два числа 5 и 16. Как мы будем складывать эти два числа? Давайте узнаем.
5 = 0 десятков + 5 единиц
16 = 1 десяток + 6 единиц.
Следовательно,
5 + 16 = 0 десятков + 5 единиц
+ 1 десятки + 6 единиц
1 десятки + 11 одному
Сейчас 11 ОДИН = 1 десятки + 1 один
Следовательно, у нас 5 + 5 + 16 = 1 десяток + 1 десяток + 1 единица = 2 десятка + 1 единица.

Следовательно, 5 + 16 = 21
Сложение с использованием десяти кадровМы можем сложить однозначное число с двузначным числом, используя десять кадров. Рассмотрим однозначные и двузначные числа и проверим представление их сложения с помощью десяти фреймов –
5 (Пять) + 12 (Двенадцать) = 17 (Семнадцать)
Вычитание чисел на десяти фреймахПроцесс Нахождение разницы между двумя числами известно как как вычитание . Другими словами, это процесс отнятия одного числа от другого. Вычитаемое число называется вычитаемым , а число, из которого вычитается вычитаемое, называется вычитаемым . Результат этого вычитания называется разностью .
Существуют различные методы, помогающие детям понять, как вычесть однозначное число из другого однозначного числа. Давайте обсудим некоторые из этих методов –
- Вычитание с использованием обратного счета
- Вычитание с использованием десяти кадров
Сравним два метода
Вычитание однозначных чисел с использованием обратного счетаПредположим, у нас есть два числа, 3 и 9.
 Мы хотим вычесть 3 из 9. Разность, которую мы получаем при вычитании, равна 6.
Мы хотим вычесть 3 из 9. Разность, которую мы получаем при вычитании, равна 6.Следовательно, 9 -3 = 6
Но что, если мы хотим сделать это наоборот? То есть мы хотим из 3 вычесть 9. Возможно ли это?
Можем ли мы вычесть большее число из меньшего числа? Вспомните числовые линии, которые вы, должно быть, изучали ранее. У них тоже есть отрицательные числа.
Когда вы вычитаете большее число из меньшего числа, вы вычитаете их целые значения и ставите знак минус (-) против разницы.
Это означает, что мы вычитаем 9 из 3, мы на самом деле вычитаем 3 из 9, где мы получаем ответ как 6 и ставим перед ним знак минус, что дает чистый ответ как -6.
Следовательно, 3 – 9 = -6
Вычитание с использованием десяти кадровМы можем вычесть одно однозначное число из другого с помощью десяти кадров. Возьмем два однозначных числа и проверим представление их вычитания с помощью десяти фреймов:
3 (три) = 2 (два) – 1 (один)
Использование десяти фреймов для понимания системы разрядовМы Знайте, что разрядное значение лежит в основе всей нашей системы счисления.
 Это система, в которой позиция цифры в числе определяет его значение. Местное значение цифры в числе — это значение, которое она занимает на месте в числе. Следовательно, число 65 471 отличается от 17 645, потому что цифры находятся в разных позициях.
Это система, в которой позиция цифры в числе определяет его значение. Местное значение цифры в числе — это значение, которое она занимает на месте в числе. Следовательно, число 65 471 отличается от 17 645, потому что цифры находятся в разных позициях.Мы также знаем, что «десять» является строительным блоком нашей системы счисления с основанием 10. Десять кадров помогают понять двузначные числа, поскольку они представляют каждую цифру в другом кадре.
Например, разница между 27 и 72 четко видна в соответствующих десяти кадрах.
Двадцать семь ( 2 7 )
Семьдесят два ( 7 2 )
Таким образом, десять рамок подходят для понимания разряда единиц и разряда десятков в разрядной системе значений.
Решенные примерыПример 1 У Питера 10 фреймов, заполненных счетчиками. Всего 100 счетчиков. Какое число обозначают соответственно синяя и розовая фишки?
Решение Нам дано представление 10 кадров, заполненных счетчиками, которые есть у Питера.
 Нам нужно найти количество синих и розовых фишек соответственно.
Нам нужно найти количество синих и розовых фишек соответственно.Мы видим, что синие счетчики заполнены в одном блоке из десяти кадров; это означает, что он представляет собой число 10
Далее идут девять розовых десяти рамок розового цвета, все они полностью заполнены. Следовательно, количество розовых фишек = 10 +10 +10 + 10 +10 + 10 + 10 + 10 + 10 = 90
Следовательно, синих фишек 10, а розовых фишек 90.
Пример 2 Какое число следующие счетчики представляют?
Решение Мы видим, что первая десятая рамка полностью заполнена; следовательно, он представляет число 10. Второй кадр из десяти пуст, что означает, что он представляет число 0. Между счетчиками есть знак « + », что означает, что нам нужно их добавить. Следовательно, у нас есть
10 + 0 = 10
Таким образом, данное расположение счетчиков представляет собой число 10
Ключевые факты и резюме- Десятичные кадры представляют собой прямоугольные кадры размером два на пять, в которые могут быть помещены такие объекты, как счетчики.
 для отображения чисел, меньших или равных десяти.
для отображения чисел, меньших или равных десяти. - Десять фреймов часто используются для обучения числам до 10.
- Десять фреймов помогают развивать чувство числа.
- Десять рамок полезны для понимания соотношения чисел, особенно для чисел от 1 до 10.
- Десять рамок помогают детям визуализировать числа, что облегчает им понимание работы с числами.
- Десять фреймов помогают детям понять, как составлять и разлагать числа.
- Сложение в математике можно определить как процесс объединения двух или более чисел вместе для получения нового итога или суммы.
- Процесс нахождения разницы между двумя числами называется вычитанием.
Десять фреймов (на тему Дня Мартина Лютера Кинга) Рабочие листы по математике
Место: Десять тысяч и сто тысяч (на тему китайского Нового года) Рабочие листы по математике
Пропустить счет (на тему Дивали) Рабочие листы по математикеМы тратим много времени на изучение и сбор информации на этом сайте.
 Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!Чувство числа «десять» и разрядное значение
Вы можете прочитать обновленную версию этой статьи в разделе «Определение числа и разрядное значение».
После того, как базовое чувство числа развилось для чисел до десяти (см. Развитие раннего чувства числа), необходимо развить сильное «чувство десяти» в качестве основы как для разрядного значения, так и для умственных вычислений. (Это не означает, что маленькие дети не осознают гораздо большие числа. причина, по которой дети не должны изучать большие числа, работая над «десятью»).
Десятичные кадры
Десятичные кадры представляют собой прямоугольные кадры размером два на пять, в которые помещаются счетчики для иллюстрации чисел, меньших или равных десяти, и поэтому они очень полезны для развития чувства числа в контексте десяти.
Использование десяти фреймов было разработано такими исследователями, как Ван де Валле (1988) и Бобис (1988). Для подсказки можно использовать различное расположение счетчиков на десяти кадрах. разные ментальные образы чисел и разные мысленные стратегии манипулирования этими числами, все в связи с отношением чисел к десяти.
Например, рассмотрите три десятикадра ниже. Какие числа изображены? Что конкретное расположение фишек побуждает вас задуматься о числах? Что вы можете сказать об отношении каждого числа к десятке?
Кадр A:
Имеется пять счетчиков; возможно, рассматривать как подгруппы из трех и двух, либо глядя на кластеры на любом конце кадра, либо глядя на числа в верхнем и нижнем рядах.
Кадр B:
Снова пять счетчиков; возможно, их можно увидеть как три в верхнем ряду и три в нижнем, или как четыре и один, или как два, два и один. Также заметно, что осталось пять пустых ящиков, форма которых аналогична полным ящикам.
 Это побуждает к осознанию того, что «пять и пять составляют десять».
Это побуждает к осознанию того, что «пять и пять составляют десять».Кадр C:
Такое расположение хорошо иллюстрирует идею о том, что «пять плюс пять — десять». Это также наводит на мысль, что половина десяти — это пять. Этот тип мышления не возник бы, если бы пять счетчиков были представлены без контекста десяти фреймов.
Большое количество упражнений с десятью фреймами позволит детям автоматически думать о числах меньше десяти с точки зрения их связи с десятью и получить прочные знания об основных фактах сложения/вычитания для десяти, которые являются неотъемлемая часть умственного счета. Например, шестилетний ребенок, когда ему показали следующий кадр из десяти, сразу сказал: «Есть восемь, потому что два отсутствует.”
У этого ребенка было сильно развито чувство числа десять и его подгрупп, и ему помогала система отсчета, обеспечиваемая системой десяти. Как только этот тип мышления установлен, десятифрейм больше не нужен.
 Хотя изначально речь идет о целых числах, мышление о числах по принципу «часть-часть-целое» поддерживает понимание дробей, в частности десятых.
Хотя изначально речь идет о целых числах, мышление о числах по принципу «часть-часть-целое» поддерживает понимание дробей, в частности десятых.
Разрядное значение
«Десять», конечно же, является строительным блоком нашей системы счисления с основанием 10. Маленькие дети обычно могут «читать» двузначные числа задолго до того, как поймут, как расположение каждой цифры влияет на ее числовое значение. Например, 5-летний ребенок может правильно прочитать 62 как шестьдесят два и 26 как двадцать шесть, и даже знать, какое число больше, не понимая, почему числа различных значений.
Десять фреймов могут стать первым шагом к пониманию двузначных чисел, просто введя второй фрейм. Размещение второго кадра справа от первого кадра, а затем введение карточек с числами будет способствовать дальнейшему развитию понимания позиционного значения.
Игры
Ten-Frame Flash (5-7 лет) 4 игрока
Материалы: дюжина десятирамок с расположением точек, пустая десятирамка для каждого ребенка, фишки.

Правила: Один ребенок показывает десятиметровую рамку, считая до трех, затем прячет ее, в то время как другие дети по памяти размещают фишки на те же позиции на своих рамочках. «Флешер» снова показывает карточку и помогает каждому ребенку проверить свой дисплей. После трех карточек следующий ребенок становится «мигалкой» и так далее, пока все не закончат свой ход.
Варианты/Дополнения:
1. За каждый правильный ответ начисляются баллы. Побеждает ребенок, набравший наибольшее количество очков.
Двадцать (5-7 лет) 3-4 игрока
Материалы: Пустые десятирамки (по 2 на ребенка), жетоны, игральные кости
Каждый ход ребенок делает бросок die, помещает это количество жетонов на свои десять фреймов, затем объявляет общее количество жетонов на фреймах. Победителем становится игрок, первым заполнивший все двадцать ячеек.Варианты/расширения:
- Каждый ход может включать в себя размещение карт с правильными цифрами под рамками.

- Каждый игрок также может объявить количество жетонов, необходимое для достижения двадцати. Точное число должно быть брошено, чтобы выиграть игру.
Угадай, что (6-8 лет) 2 игрока
Материалы: пустые десятирамочные рамки, фишки, большие книги в твердом переплете для создания барьера между парами детей.
Правила: Один игрок тайно расставляет фишки на десятке. Другой игрок задает вопросы, на которые можно ответить «да» или «нет», пытаясь получить достаточно подсказок, чтобы определить расположение фишек. Например: Верхний ряд заполнен? Есть 8 счетчиков? В нижнем ряду есть пустая ячейка?
Варианты/Дополнения:
1. По мере того, как игроки становятся более опытными, можно подсчитывать количество вопросов. Побеждает игрок, задавший меньше вопросов.
Ссылки
Van de Walle, J. (1988). Раннее развитие числовых отношений. Учитель арифметики. Том 35, 15-21 февраля.


 Следующая страница.
Следующая страница.


 Мы хотим вычесть 3 из 9. Разность, которую мы получаем при вычитании, равна 6.
Мы хотим вычесть 3 из 9. Разность, которую мы получаем при вычитании, равна 6. Это система, в которой позиция цифры в числе определяет его значение. Местное значение цифры в числе — это значение, которое она занимает на месте в числе. Следовательно, число 65 471 отличается от 17 645, потому что цифры находятся в разных позициях.
Это система, в которой позиция цифры в числе определяет его значение. Местное значение цифры в числе — это значение, которое она занимает на месте в числе. Следовательно, число 65 471 отличается от 17 645, потому что цифры находятся в разных позициях. Нам нужно найти количество синих и розовых фишек соответственно.
Нам нужно найти количество синих и розовых фишек соответственно. для отображения чисел, меньших или равных десяти.
для отображения чисел, меньших или равных десяти. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
 Это побуждает к осознанию того, что «пять и пять составляют десять».
Это побуждает к осознанию того, что «пять и пять составляют десять».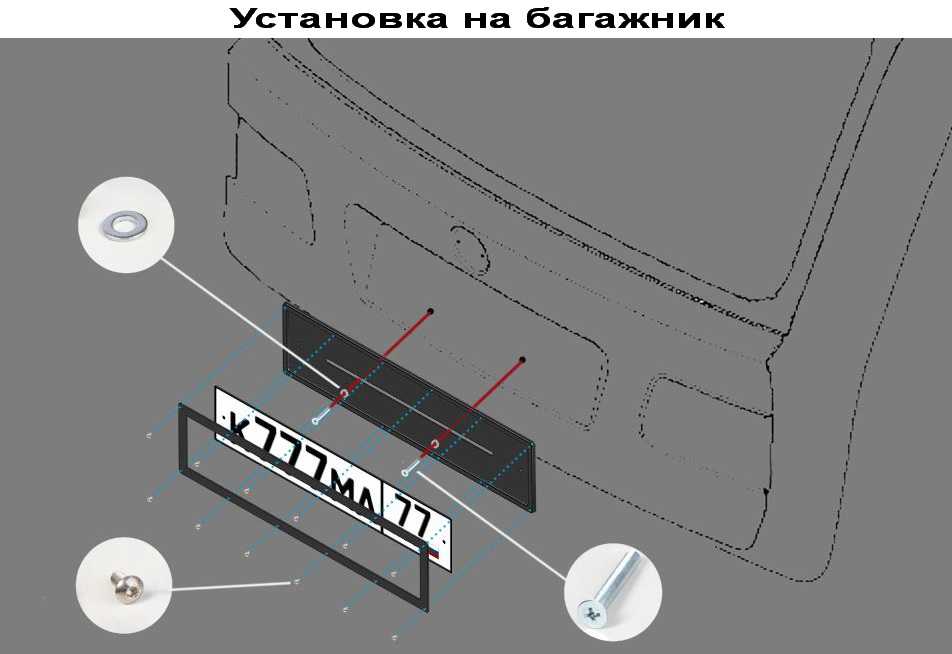 Хотя изначально речь идет о целых числах, мышление о числах по принципу «часть-часть-целое» поддерживает понимание дробей, в частности десятых.
Хотя изначально речь идет о целых числах, мышление о числах по принципу «часть-часть-целое» поддерживает понимание дробей, в частности десятых. 

