Ни о какой безапелляционности в моих высказываниях не может быть и речи! — ЖЖ
?
| ||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
В точности.
Это обычные часы.
Если стрелки совпали на цифре 12, через 65 минут часовая стрелка прошла несколько дальше цифры 1, и минутная должна с ней совпать более, чем через 65 минут.Эмоциональная нестабильность-эмоциональная стабильность по Кеттеллу
3.
Фактор С: «эмоциональная нестабильность-эмоциональная стабильность»Этот фактор характеризует динамическое обобщение и зрелость эмоций в противоположность нерегулируемой эмоциональности. Психоаналитики пытались описать этот фактор как эго-силу и эго-слабость. Согласно методике Кеттелла, личность с полюсом C- легко раздражается из-за тех или иных событий или людей, не удовлетворена жизненными ситуациями, собственным здоровьем, кроме того, это личность безвольная. Однако такая интерпретация достаточно ортодоксальна, поскольку здесь не учитывается пластичность эмоциональной сферы. Люди с высокой оценкой по фактору C+ чаще являются лидерами, чем те, чьи показатели по этому фактору ближе к полюсу C-. С другой стороны, у руководящего состава диапазон показателей по фактору С широк; некоторым из них присущи низкие значения по этому фактору (возможно, здесь сказывается реакция усталости и озабоченность при стрессе).
Установлено, что людям с высокой и средней оценкой по фактору С свойственны и более высокие моральные качества.
В целом фактор имеет генетическое происхождение и направлен на измерение эмоциональной стабильности; он в большой степени соотносится с понятиями слабой и сильной нервной системы (по И.П.Павлову).
Профессиями, требующими преодоления стрессовых ситуаций (руководители, летчики, спасатели и т. д.), должны владеть индивидуумы с высокими оценками по фактору С. В то же время в профессиях, где не требуется быстрого принятия решений, эмоциональной стабильности и где можно решать вопрос самому (художники, почтальоны и т. д.), можно иметь и низкие оценки по этому фактору.
- 1-3 стена – имеется низкий порог в отношении фрустрации, изменчивый и пластичный, избегающий требований действительности, невротически утомляемый, раздражительный, эмоционально возбудимый, имеющий невротическую симптоматику (фобии, нарушения сна, психосоматические расстройства). Низкий порог свойствен всем формам невротических и некоторым психическим расстройствам.
- 4 стена – чувствительный, эмоционально менее устойчивый, легко расстраивается.
- 7 стенов – эмоционально устойчивый, трезво оценивающий действительность, активный, зрелый.
- 8-10 стенов – эмоционально зрелый, устойчивый, невозмутимый. Высокая способность к соблюдению общественных моральных норм. Иногда смиренная покорность перед нерешенными эмоциональными проблемами. Хороший уровень «С» позволяет адаптироваться даже при психических расстройствах.
Вопросы к Фактору С
4. Когда я ложусь спать, то:
- засыпаю быстро;
- когда как;
- засыпаю с трудом;
21. У меня, как правило, хватает энергии, когда мне это необходимо:
- да;
- трудно сказать;
- нет;
38. То, что в некоторой степени отвлекает моё внимание:
- раздражает меня;
- нечто среднее;
- не беспокоит меня совершенно;
55. То, что я делаю, у меня не получается:
- редко;
- время от времени;
- часто;
72.
Иногда у меня бывают непродолжительные приступы тошноты и головокружения без определённой причины:
- да;
- иногда;
- нет;
89. Если стрелки часов встречаются ровно через каждые 65 мин., отмеренных по точным часам, то эти часы:
- отстают;
- идут правильно;
- спешат;
Если стрелки часов совпадают каждые 65 минут (верно
Главная » Aptitude » Часы и календари » Вопрос
Часы и календари
Простые вопросы
Умеренные вопросы
D трудные вопросы
Часы и календари Учебник
Способности
Система счисления
Упрощение
Дроби
Элементарная алгебра
LCM и HCF
Среднее значение
Аппроксимация
Унитарный метод
Линейное уравнение
Квадратное уравнение
Скидка
кубический кореньПорядок величины
Прибыли и убытки
Odd Man Out and Series
Работа и заработная плата
Алгебра
Акции и доли
Истинная скидка
Соотношение, доля
Партнерство
Аллигация или смесь
Время и работа
Трубы и цистерна
Скорость, время и расстояние
Проблема с поездами
Высота и расстояние
Банковская скидка
Лодки и ручьи
Гонки и игры
Задачи на века
Часы и Календари
Простые проценты
Сложные проценты
Множества и функции
Площадь и периметр
Объем и площадь поверхности твердых фигур
Последовательности и ряды
Плоская геометрия
Логарифм
Вероятность
Перестановка и комбинация
Статистика
Измерение
Тригонометрия
Способность разное
Если стрелки часов совпадут через каждые 65 минут (истинное время), то через 24 часа часы получат:
10 10 минут. 143 9 12 мин. 143 11 12 мин. 143 12 10 минут. 143
Правильный вариант: A
По заданному выше вопросу можно сказать, что
| Минутная стрелка увеличивает 60 минут в | 60 | x 60 | = | 720 | = 65 | 5 | минут. |
| 55 | 11 | 11 |
| ∴ Стрелки правильных часов совпадают каждые 65 | 5 | минут. |
| 11 |
| Часы, о которых идет речь, выигрывают | 5 | минут за 65 минут. |
| 11 |
| Требуемый ответ = | 5 | х | 1 | х | 24 х 60 = | 1440 | = | минут = 10 | 10 | минут |
| 11 | 65 | 143 | 143 |
Часы (обновлено)
Циферблат часов представляет собой окружность, окружность которой разделена на 12 частей, называемых часовыми пространствами.
Каждое часовое пространство далее делится на 5 частей, называемых минутными пространствами. Таким образом, вся окружность делится на 12 х 5 = 60 минут. Время, затрачиваемое часовой стрелкой (меньшая стрелка) на преодоление расстояния в один час, равно времени, за которое минутная стрелка (более длинная стрелка) проходит расстояние, равное всей окружности. Таким образом, мы можем заключить, что за 60 минут минутная стрелка опережает часовую на 55 минут.
Примечание. Приведенное выше утверждение (подчеркнуто) очень полезно при решении задач в этой главе, поэтому его следует запомнить. Вышеупомянутое утверждение хочет сказать, что:
« За час часовая стрелка проходит расстояние в 5 минут, а минутная стрелка — на расстояние в 60 минут. Таким образом, минутная стрелка опережает часовую на 60 – 5 = 55 минут».
Некоторые другие факты:
1. В каждый час обе стрелки совпадают один раз.
2. Когда две стрелки находятся под прямым углом, расстояние между ними составляет 15 минут.
Это происходит два раза в каждый час.
3. Когда стрелки находятся в противоположных направлениях, расстояние между ними составляет 30 минут. Это происходит раз в каждый час.
4. Стрелки находятся на одной прямой, когда они совпадают или противоположны друг другу.
5. Часовая стрелка проходит по всей окружности часов один раз за 12 часов. Таким образом, минутная стрелка движется в двенадцать раз быстрее, чем часовая. 90}$ друг от друга. Следовательно,
Слишком быстро и слишком медленно :
Если часы показывают 9:20, когда правильное время 9:10, говорят, что они на 10 минут быстрее. И если говорят, что это на 10 минут быстрее. И если он показывает 9.00, когда правильное время 9.10, говорят, что оно на 10 минут медленнее.
2 важных метода сокращения:
Угол между часовой и минутной стрелками в данный момент времени Ч:ММ определяется выражением $\theta = \left| {30 \times H – \displaystyle\frac{{11}}{2} \times MM} \right|$
Время после H часов, часовая и минутная стрелки находятся на $\theta $ градусов = $MM = \displaystyle\frac{2}{{11}} \times \left( {30 \times H \pm \theta } \right)$
Помните, что любой угол меньше 180 градусов встречается 2 раза за 24 часа.
0}$. Чтобы получить 90}}} = \displaystyle\frac{{90}}{{\displaystyle\frac{{11}}{2}}} = 90 \times \displaystyle\frac{2}{{11}} = \displaystyle\ frac{{180}}{{11}} \Rightarrow 16\displaystyle\frac{4}{{11}}$ минут
Альтернативный метод:
Используйте формулу $\theta $ градусов = $MM = \displaystyle\frac {2}{{11}} \times \left( {30 \times H \pm \theta } \right)$
$MM = \displaystyle\frac{2}{{11}} \times \left( { 30 \times 3 \pm 0} \right) = \displaystyle\frac{{180}}{{11}} = 16\displaystyle\frac{4}{{11}}$ min
2. В какое время между 7 и 8 часами стрелки часов будут на одной прямой, но не вместе?
Когда стрелки часов находятся на одной прямой, но не вместе, расстояние между ними составляет 30 минут. В 7 часов они составляют 25 мин. пробелы друг от друга.
Минутной стрелке нужно будет набрать всего 5 мин. мест
55 мин. места набираются за 60 мин.
5 мин. пробелы получаются в $\left( {\displaystyle\frac{5}{{55}} \times 60} \right)$$ \Rightarrow 5\displaystyle\frac{5}{{11}}$ мин.
прошлое 7 90}}} = \displaystyle\frac{{30}}{{\displaystyle\frac{{11}}{2}}} = 30 \times \displaystyle\frac{2}{{11}} = \displaystyle\ frac{{60}}{{11}} \Rightarrow 5\displaystyle\frac{5}{{11}}$
Альтернативный метод:
Используйте формулу $\theta $ градусов = $MM = \displaystyle\frac{2 }{{11}} \times \left( {30 \times H \pm \theta } \right)$
$MM = \displaystyle\frac{2}{{11}} \times \left( {30 \times 7 \pm 180} \right)$ = $\displaystyle\frac{{210 \pm 180}}{{11}}$ = $\displaystyle\frac{{390}}{{11}}$ или $\displaystyle \frac{{30}}{{11}}$
Мы отклоняем $\displaystyle\frac{{390}}{{11}}$, так как часовая и минутная стрелки находятся на 0 градусов.
3. Минутная стрелка часов обгоняет часовую с интервалом в 65 минут точного времени. Сколько часы прибавляют или теряют в день?
Если часы идут вовремя, их часовая и минутная стрелки точно совпадают для каждого ${\rm{65}}\displaystyle\frac{{\rm{5}}}{{{\rm{11}}} }$ мин.
Но в этих часах обе стрелки встречаются с интервалом в 65 минут.
так что эти часы выигрывают время.
или 65 минут в правильных часах = ${\rm{65}}\displaystyle\frac{{\rm{5}}}{{{\rm{11}}}}$ минут в этих часах.
Или за каждые 65 минут эти часы отстают на 5/11 минут.
за каждую минуту, когда эти часы отстают $\displaystyle\frac{5}{{11}} \times \frac{1}{{65}}$
За 24 часа или 1 440 минут они отстают = $\displaystyle\frac{ 5}{{11}} \times \frac{1}{{65}} \times 24 \times 60$ = $10\displaystyle\frac{{10}}{{143}}$
Альтернативно:
Минута стрелка часов обгоняет часовую стрелку с интервалом в M минут правильного времени. Часы отстают или отстают за день на $\left( {\dfrac{{720}}{{11}} – M} \right)\left( {\dfrac{{60 \times 24}}{M}} \right)$ минут.
4. Часы, которые отсчитывают время равномерно, отстают на 5 минут в 8 часов утра в воскресенье и спешат на 5 минут 48 секунд в 8 часов вечера следующего воскресенья. Когда это было правильно?
В это воскресенье утром в 8:00, на часах 5 мин. Медленно, а в следующее воскресенье в 20:00 оно становится быстрым на 5 минут 48 секунд.
Часы получают 5 + ${\rm{5}}\displaystyle\frac{{{\rm{48}}}}{{{\rm{60}}}}$ = $\displaystyle\frac{{54} {5}$ мин за время $\left( {{\rm{7 \times 24}}} \right){\rm{ + 12}}$ = 180 часов.
Чтобы отобразить правильный зубец, он должен увеличиться на 5 мин.
$\displaystyle\frac{{54}}{5}$ мин ——- 180 часов
5 мин ——-?
$ \Rightarrow \frac{5}{{\dfrac{{54}}{5}}} \times 180$
$ \Rightarrow 83\frac{1}{3}$hrs = 72hrs + $11\dfrac{1 {3}$hrs = 3 дня + 11 часов + 20 минут
Таким образом, правильное время будет показано в среду в 19:20
5. Часы настроены точно на 8:00. Часы отстают на 10 минут за 24 часа. Каким будет истинное время, когда часы покажут 13:00 следующего дня? 901:21 Между 8:00 и 13:00 прошло всего 29 часов.
Эти часы показывают 24 часа 10 минут или $\displaystyle\frac{{{\rm{145}}}}{{\rm{6}}}$ в течение 24 часов в правильных часах. Через 29 часов в этих часах = $\displaystyle\frac{{29}}{{\displaystyle\frac{{{\rm{145}}}}{{\rm{6}}}}} \times 24$ часов в фактических часах = $\displaystyle\frac{{144}}{5}$ = $28\displaystyle\frac{4}{5}$ = 28 часов 48 минут.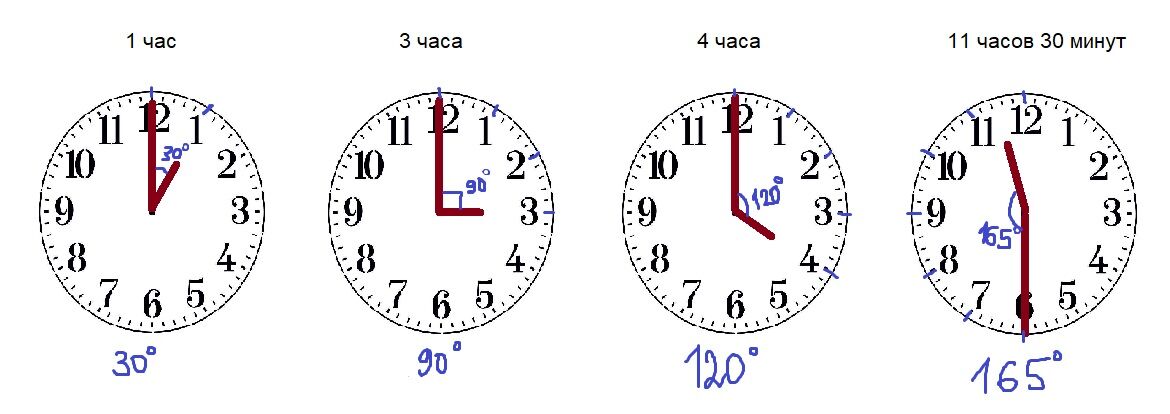
Значит, фактическое время 12:48
6. Сколько теряют часы в день, если их стрелки совпадают каждые 64 минуты?
Ответ: Если часы идут вовремя, их часовая и минутная стрелки совпадают точно для каждого ${\rm{65}}\displaystyle\frac{{\rm{5}}}{{{\rm{11} }}}$ мин.
Но в этих часах обе стрелки встречаются с интервалом в 64 минуты. Таким образом, эти часы 90 324 ускоряют время.
или 64 минуты в правильных часах = ${\rm{65}}\displaystyle\frac{{\rm{5}}}{{{\rm{11}}}}$ минут в этих часах.
Или каждые 64 минуты эти часы прибавляют $1\dfrac{5}{{11}}$ минут. или $\dfrac{{16}}{{11}}$ минут 90 121 За каждую минуту эти часы отстают $\dfrac{{16}}{{11}} \times \dfrac{1}{{64}}$
За 24 часа или 1440 минут он получает = $\dfrac{{16}}{{11}} \times \dfrac{1}{{64}} \times 1440$ = 32$\dfrac{8}{{11} }$ минут
Альтернативно:
Минутная стрелка часов обгоняет часовую с интервалом в M минут правильного времени. Часы отстают или отстают за день на $\left( {\dfrac{{720}}{{11}} – M} \right)\left( {\dfrac{{60 \times 24}}{M}} \right)$ минут.
$ \Rightarrow \left( {\dfrac{{720}}{{11}} – M} \right)\left({\dfrac{{60 \times 24}}{M}} \right)$ = $ \left( {\dfrac{{720}}{{11}} – 64} \right)\left( {\dfrac{{60 \times 24}}{{64}}} \right)$ = $ \dfrac {{16}}{{11}}\left( {\dfrac{{60 \times 3}}{8}} \right) = \dfrac{2}{{11}}\left( {60 \times 3 } \right)$ = $ \dfrac{{360}}{{11}} = 32\dfrac{8}{{11}}$
Уровень – 2
и 17:00 вернулся между 17:00 и 18:00 и обнаружил, что стрелки его часов точно поменялись местами. Когда он вышел?
Мы знаем, что циферблат часов имеет 60 равных делений (минутных делений). За один час минутная стрелка делает один полный оборот, т. е. проходит 60 делений, а часовая — 5 делений. Предположим, что, когда человек вышел, часовая стрелка была на x делений вперед после 4 часов. Также предположим, что когда человек вернулся, часовая стрелка была на y делений впереди 5′ часов.
Мы знаем, что скорости часовой и минутной стрелок находятся в соотношении 1 : 12.
Из приведенной выше диаграммы видно, что за время, которое часовая стрелка проходит x делений, часовая стрелка проходит 25 + y делений. (рассчитывать от 4 часов)
$ \Rightarrow \displaystyle\frac{1}{{12}} = \displaystyle\frac{x}{{25 + y}}$ ———– (1)
Также в время часовая стрелка перемещается на y делений, минутная стрелка перемещается на 10 + x делений (рассчитывать от 5′ часов)
$ \Rightarrow \displaystyle\frac{1}{{12}} = \displaystyle\frac{y}{{20 + x}}$ ———– (2)
Из уравнения (1) получаем 25 + y = 12x, а из уравнения (2) получаем 20 + x = 12y или x = 12 y – 20
Подстановка значения x в уравнение (1)
$ \Rightarrow $25 + y = 12 (12y – 20)
$ \Rightarrow $25 + y = 144y – 240
$ \Rightarrow $143 y = 265
$ \Rightarrow $ y = $1\displaystyle\frac{{122}}{{143}}$
Итак, человек вышел на y делений после 5. Таким образом, 25 + $1\displaystyle\frac{{122}}{{143}}$ 90 121 Таким образом, время, когда он вышел из дома = 4 часа $26\displaystyle\frac{{122}}{{143}}$
Альтернативный метод:
Из приведенной выше диаграммы видно, что часовая и минутная стрелки вместе покрывают 60-минутные интервалы.
Мы знаем, что скорости часовой и минутной стрелок относятся как 1 : 12. Таким образом, наша из этих 60-минутных промежутков часовая стрелка покрыла бы $60 \times \displaystyle\frac{1}{{13}} = 4\ displaystyle\frac{8}{{13}}$ минутных пробелов.
т. е. минутная стрелка стоит на $4\displaystyle\frac{8}{{13}}$ минутных интервалов впереди часовой стрелки, когда человек вышел.
В 4 часа. Минутная стрелка отстает от часовой на 20 минутных делений. Когда мужчина вышел, часовая стрелка опережала часовую стрелку на $4\displaystyle\frac{8}{{13}}$. Таким образом, он получил 20 + $4\displaystyle\frac{8}{{13}}$ = 20 + $\displaystyle\frac{{60}}{{13}}$ = $\displaystyle\frac{{320}} {{13}}$
Но мы знаем, что минутная стрелка смещается на 55 минут по сравнению с часовой стрелкой за 60 минут.
Занимает 1 минуту за $\displaystyle\frac{{60}}{{55}}$ минут.
Чтобы получить $\displaystyle\frac{{320}}{{13}}$ минут, требуется $\displaystyle\frac{{320}}{{13}} \times \displaystyle\frac{{60}}{ {55}} = 26\displaystyle\frac{{122}}{{143}}$ минут.
Итак, мужчина ушел в 4 часа $26\displaystyle\frac{{122}}{{143}}$ минут.
8. Лица, вышедшие из дома между 14:00 и 14:00. и 15:00 вернулся между 16:00 и 17:00 и обнаружил, что стрелки его часов точно поменялись местами. Сколько времени он отсутствовал?
В этом вопросе часовая и минутная стрелки вместе покрывают 120 минут. (от 2:мм до 4:мм)Из них минутная стрелка покрывала бы 12/13 часть.
Таким образом, общее время, в течение которого он вышел, определяется как $ \Rightarrow 120 \times \displaystyle\frac{{12}}{{13}} = 110\frac{{10}}{{13}}$ минут.
9. Между 5 и 6 часами женщина посмотрела на часы и, приняв часовую стрелку за минутную, подумала, что она на 57 минут раньше, чем нужное время. Когда было правильное время?
Итак, правильное время = 5: 12x или (300 + 12x) минут
Но на этот раз она ошиблась и приняла 4 : (25 + x) или (265 + x) минут
$ \Rightarrow $ (300 + 12x) – ( 265 + x) = 57 минут
$ \Rightarrow $ x = 12 минут
Таким образом, правильное время = 5: 24 минуты.
10. Когда его спросили о времени, Амит ответил; «Если вы прибавите одну четверть времени с полуночи до настоящего момента к половине времени с этого момента до следующей полуночи, вы получите время». который час?
Пусть время будет “t” часов. С полуночи до этого времени прошло «t» часов. От настоящего момента до следующей полуночи (24-t) часов.
Теперь $\displaystyle\frac{t}{4} + \frac{{24 – t}}{2} = t \Rightarrow \frac{{t + 48 – 2t}}{4} = t$
$ \Rightarrow 48 – t = 4t$
$ \Rightarrow 5t = 48 \Rightarrow t = \displaystyle\frac{{48}}{5}$часов или $9\displaystyle\frac{3}{5}$ часов
11 Жители планеты Раху измеряют время в часах и минутах, которые отличаются от часов и минут нашей земли. Их день состоит из 36 часов, в каждом часе 120 минут. Циферблаты их часов показывают 36 часов. Каков угол между часовой стрелкой и минутной стрелкой рауианских часов, когда они показывают время 9:48? [Рахуанцы измеряют углы в градусах, как мы это делаем на Земле. Но для них угол вокруг точки составляет 720 градусов вместо 360 градусов.