Чикирис игорь геннадьевич: Игорь Чикирис возглавил «ЭфСиЭй Рус» | Новости

АО “ЭФСИЭЙ РУС”, г. Москва, ИНН 7714702142, контакты, реквизиты, финансовая отчётность и выписка из ЕГРЮЛ

+7 495 745-26-36
+7 495 153-41-54
+7 495 154-38-53
+ ещё 2

[email protected]

chrysler.ru

---

Контактная информация неактуальна?

Редактировать

---

Юридический адрес

105120, г. Москва, пер. 2-й Сыромятнический, д. 1, помещ. 107

Показать на карте

ОГРН	1077757577402
ИНН	7714702142
КПП	770901001
ОКПО	81482618

Код ОКОГУ	4210011 Хозяйственные общества и товарищества с участием иностранных юридических и (или) физических лиц, а также лиц без гражданства
Код ОКОПФ	12267 Непубличные акционерные общества
Код ОКФС	23 Собственность иностранных юридических лиц
Код ОКАТО	45277556000 Беговой
Код ОКТМО	45334000000 муниципальный округ Беговой

Регистрация в ФНС

Регистрационный номер 1077757577402 от 5 июля 2007 года

Межрайонная инспекция Федеральной налоговой службы №46 по г. Москве

Регистрация в ПФР

Регистрационный номер 087102122045 от 2 августа 2021 года

Государственное учреждение – Главное Управление Пенсионного фонда РФ №10 Управление №2 по г. Москве и Московской области муниципальный район Таганский г. Москвы

Регистрация в ФСС

Регистрационный номер 772003575277201 от 6 июля 2007 года

Филиал №20 Государственного учреждения – Московского регионального отделения Фонда социального страхования Российской Федерации

45.11.1	Торговля оптовая легковыми автомобилями и легкими автотранспортными средствамиОСНОВНОЙ
45.19.1	Торговля оптовая прочими автотранспортными средствами
45.11.2	Торговля розничная легковыми автомобилями и легкими автотранспортными средствами в специализированных магазинах
73.11	Деятельность рекламных агентств
45.11.3	Торговля розничная легковыми автомобилями и легкими автотранспортными средствами прочая
45. 20	Техническое обслуживание и ремонт автотранспортных средств
77.39	Аренда и лизинг прочих видов транспорта, оборудования и материальных средств, не включенных в другие группировки
68.3	Операции с недвижимым имуществом за вознаграждение или на договорной основе

+ ещё 7

Финансовая отчётность АО “ЭФСИЭЙ РУС” согласно данным ФНС и Росстата за 2011–2021 годы

Финансовые результаты за 2021 год

Выручка	Чистая прибыль	Капитал
9,4 млрд ₽ 46%	1,5 млрд ₽ 417%	3,2 млрд ₽ 93%

Бухгалтерская отчётность за все доступные периоды

---

Показатели финансового состояния за 2021 год

• Коэффициент автономии (финансовой независимости) 0. 71
• Коэффициент обеспеченности собственными оборотными средствами 0.69
• Коэффициент покрытия инвестиций 0.72

• Коэффициент текущей ликвидности 3. 34
• Коэффициент быстрой ликвидности 2.91
• Коэффициент абсолютной ликвидности 2.57

• Рентабельность продаж 16. 3%
• Рентабельность активов 34.0%
• Рентабельность собственного капитала 48.0%

Сравнительный финансовый анализ за 2021 годНОВОЕ

Уплаченные АО “ЭФСИЭЙ РУС” – ИНН 7714702142 – налоги и сборы за 2021 год

Страховые взносы на обязательное социальное страхование на случай временной нетрудоспособности и в связи с материнством	1,8 млн ₽
Налог на прибыль	198,6 млн ₽
Транспортный налог	2,3 млн ₽
Страховые и другие взносы на обязательное пенсионное страхование, зачисляемые в Пенсионный фонд Российской Федерации	28,8 млн ₽
Налог на добавленную стоимость	640,9 млн ₽
Страховые взносы на обязательное медицинское страхование работающего населения, зачисляемые в бюджет Федерального фонда обязательного медицинского страхования	9 млн ₽
Итого	881,4 млн ₽

Согласно данным ФНС, среднесписочная численность работников за 2021 год составляет
62 человека

2021 г.	62 человека	294,2 тыс. ₽
2020 г.	66 человек	271,1 тыс. ₽
2019 г.	71 человек	258,8 тыс. ₽

Значения рассчитаны автоматически по финансовым показателям оплаты труда и среднесписочной численности АО “ЭФСИЭЙ РУС”, эта информация может быть неточной

Компания АО “ЭФСИЭЙ РУС” опубликовала 1 сообщение и является участником 1 сообщения на Федресурсе

Типы сообщений

Результаты обязательного аудита

1

Согласно данным ФГИС “Единый Реестр Проверок”, с 2015 года в отношении АО “ЭФСИЭЙ РУС” были инициированы 2 проверки

1	без нарушений
1	выявлены нарушения
0	результатов ещё нет

Последняя проверка

Внеплановая документарная проверка № 772105341779 от 1 февраля 2021 года

Проверку проводит Государственная инспекция труда в городе Москве

Выявлены нарушения

Согласно данным картотеки арбитражных дел, в арбитражных судах РФ были рассмотрены 47 судебных дел с участием АО “ЭФСИЭЙ РУС”

33	в роли истца
14	в роли ответчика

Последнее дело

№ А50-19092/2022 от 1 августа 2022 года

Экономические споры по гражданским правоотношениям

Истец

ИП Говорущенко Сергей Викторович

Ответчик

АО “ЭФСИЭЙ РУС”

Согласно данным ФССП на 1 февраля 2023 года, в отношении АО “ЭФСИЭЙ РУС” открыто 9 исполнительных производств

Общая сумма	80 тыс. ₽
Непогашенная задолженность	0 ₽

Типы исполнительных производств

Исполнительские сборы	8
Прочее	1

Возможны частичные совпадения по названию и адресу, настоятельно рекомендуем проверить информацию на сайте ФССП

Полная хронология важных событий с 5 июля 2007 года

	27.03.2020 Сдана финансовая отчётность за 2019 год
	09.09.2020 Патриньяни Лука больше не является генеральным директором организации Чикирис Игорь Геннадьевич становится новым генеральным директором организации
	19.03.2021 Сдана финансовая отчётность за 2020 год
	27.07.2021 КПП изменен с 771401001 на 770901001
	Юридический адрес изменен с 125284, г. Москва, пр-т Ленинградский, д. 31А, стр. 1, этаж 22 пом. I комната 1 на 105120, г. Москва, МО Таганский, пер. 2-й Сыромятнический, д. 1, помещ. 85
	Удалена запись об учредителе Хике Франк Петер Удалена запись об учредителе ЗАКРЫТОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО “ДАЙМЛЕРКРАЙСЛЕР АВТОМОБИЛИ РУС”
	02.08.2021 Регистрация в ПФР, присвоен регистрационный номер 087102122045 Государственное учреждение – Главное Управление Пенсионного фонда РФ №10 Управление №2 по г. Москве и Московской области муниципальный район Таганский г.Москвы
	31.03.2022 Сдана финансовая отчётность за 2021 год
	08.06.2022 Юридический адрес изменен с 105120, г. Москва, МО Таганский, пер. 2-й Сыромятнический, д. 1, помещ. 85 на 105120, г. Москва, МО Таганский, пер. 2-й Сыромятнический, д. 1, помещ. 107

Похожие компании

ООО “АВТО ОЛИМП” г. Смоленск, Смоленская область	6732024498
ООО “ФИРМА РУС-ЛАН” г. Москва	7728612770
ООО “АВТОСАЛОН “ТАМБОВТЕХЦЕНТР” г. Тамбов, Тамбовская область	6829020514
ООО “АЛЬФА ТРАК” Московская Область, Московская область	5035042681
ООО “ЮФА” СНГ г. Санкт-Петербург	7820302690
ООО “ТЕХТРЕЙД” г. Челябинск, Челябинская область	7450065628
ООО “АНГАР-67” г. Смоленск, Смоленская область	6730082039

Авто для ценителей качества | Архив

27.03.2013 00:00

Примерное время чтения: 4 минуты

113

Еженедельник “Аргументы и Факты” № 13. Аргументы и факты – Тверь 27/03/2013

В Твери открылся новый салон Volkswagen

На минувшей неделе в столице Верхневолжья состоялось знаменательное событие – открытие автосалона “Фольксваген Центр Макон Авто”. Новый центр является преемником уже знакомого тверича-нам официального дилера Volkswagen “Макон Авто”, успешно работающего в Твери на протяжении пяти лет. Отметить появление салона европейского уровня собрались друзья, партнёры и почитатели автомобилей безупречного качества.

Салон на пять с плюсом

Открытие нового дилерского центра прошло ярко и со вкусом. Ещё при входе в салон гости отметили незаурядный стиль здания, выдержанный в корпоративном духе Volkswagen. Но особенно впечатлил собравшихся сам шоу-рум. Лаконичный, современный интерьер, просторная и комфортная клиентская зона, удобное месторасположение и собственный сервисный центр, оснащённый по последнему слову техники, -в салоне всё предусмотрено для максимального удобства жителей Верхневолжья. В распоряжении покупателей предоставлено 800 квадратньгх метров, вместивших в себя всю модельную линейку легковых и коммерческих автомобилей. Отдельно выделена зона торжественной выдачи автомобиля владельцу. Каждая мелочь в помещении радует глаз. Поздравить “Макон Авто” с замечательным прибавлением в

семействе приехал Игорь ЧИКИРИС, руководитель отдела продаж Volkswagen Легковые автомобили в России.

– Это важное событие в жизни всего концерна и, конечно же, Верхневолжья. Мы гордимся тем, что наши автомобили очень любят по всей стране и особенно в Тверской области, – высказался Игорь Геннадьевич. – Volkswagen – одна из лучших марок, которая заслуживает самых высоких наград. В этом году, например, легендарный Volkswagen Golf получил престижную премию – звание “Автомобиль года”. И при этом авто доступен всем. Любой желающий может по достоинству оценить эргономичность и надёжность немецких машин, придя в салон к официальному дилеру.

Сервис – от “а” до “я”

Безусловно, в основу нового центра легли столпы, делающие марку Volkswagen узнаваемой уже на протяжении нескольких десятилетий – сочетание высокой технологической оснастки, современного дизайна, квалифицированных продаж и сервиса. Здесь горожане могут не только приобретать, но и обслуживать свои автомобили. Для этих целей в салоне создан крупный сервисный центр площадью 2000 квадратных метров, оснащённый передовыми технологиями. Он укомплектован интерактивной приёмкой, 15 автоподъёмниками, диагностическим оборудованием, в наличии все необходимые запчасти. Полная оснастка позволяет оперативно и качественно проводить все виды ремонта автомобилей. Для большинства автовладельцев это неоспоримое преимущество.

– В нашей семье две машины – Touareg и Passat, и открытие нового дилерского центра нас очень порадовало. С удовольствием пришли на праздник, – признался Алексей ИВАНОВ, клиент компании. – Я много лет дружу с “Макон Авто” и могу без ложной скромности сказать – люди тут работают замечательные. Атмосфера всегда дружеская. Приходишь в салон, словно к себе домой, и всегда с уверенностью, что обслуживание пройдёт по высшему разряду.

Действительно, не только современные технологии и инновации, но и люди, работающие в центре, поддерживают высокую планку Volkswagen. В компании трудятся настоящие профессионалы своего дела. У команды автосалона за плечами серьёзный послужной список достижений: это и попадание в десятку лучших дилерских предприятий страны, и лучший показатель по продажам автомобилей, и диплом “Зелёный автосервис” города Твери, а также большое количество других наград.

– За прошедшие пять лет мы получили отличный опыт работы с концерном Volkswagen и сумели попасть в десятку лучших дилерских центров в России. Учитывая то, что наш центр построен по самым новым технологиям, которые специально были разработаны концерном, мы готовы предложить своим клиентам ещё более высокий уровень обслуживания и полную линейку автомобилей нашей марки. Вы можете прийти к нам в салон и выбрать любой автомобиль – от легкового до коммерческого, – рассказал Константин ШАВЛЮКЕВИЧ, директор “Фольксваген Центра Макон Авто”.

Торжество, посвящённое появлению нового салона “Фольксваген Центра Макон Авто” в Твери, прошло на одном дыхании.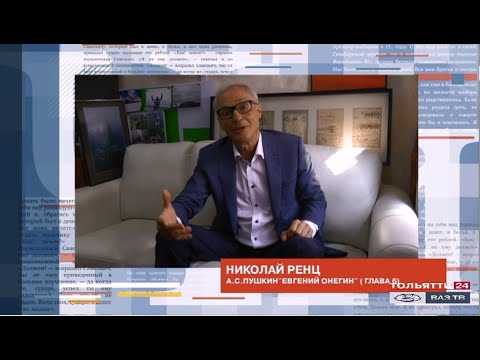 Это был не просто праздник, а вечер совпадения предпочтений всех тех, кто ценит безупречное качество и комфорт. Всё это объединила в себе марка Volkswagen. Для её поклонников надёжность – не просто слово, а стиль жизни.

“Фольксваген Центр Макон Авто”

Адрес: 170040, Тверская обл, г. Тверь, пр-т 50 лет Октября, 5 Телефон 8 (4822) 62-62-62

Web-сайт: https://www.makonauto.ru

• Не мармелад, а сказка! →
• SKODA едет в Удомлю →
• Класс – “комфорт”! →

Следующий материал

Также вам может быть интересно

• Праздник высокой марки
• Блестящая работа! «Александрит №1» взял Гран-при профессионального конкурса
• Андрей Дементьев: “Дом поэзии открыт для всех нас”
• Добро пожаловать в сказку! В Тверской области откроется музей мармелада
• Здоровье в надёжных руках

Новости smi2. ru

Цифровой архив Детройтских еврейских новостей – 24 июня 1966 г.

Отказ от ответственности: Сгенерированный компьютером простой текст может содержать ошибки. Узнайте больше об этом.

=:

THE DETROIT JEWISH NEWS

Яркие роли израильтян в фильмах,
«Арабеск», новый шпионский триллер «Здесь заслуживают внимания разоблачения нацистских преступлений»

30 — пятница, 24 июня 1966 г.

(Авторское право, 1966, JTA, Inc.)0012 Spirit Is Willing» на студии Paramount
в Голливуде. Другие актеры возглавляют Вера Майлз, мальчик-
чудо Барри Гордон (из «
Тысяча клоунов»), Джон Мак-
Гивер, Джилл Таунсенд, Касс Дейли,
Рики Корделл, Мэри Уикс, Джесси
Уайт, Харви Лембек, Боб Дон-
нер и Дж. К. Флиппен, а также приглашенная звезда
в телесериале
Джон Эстин. на основе Натаниэля Бенчли 9Роман 0012 “Посетители”.
*
*
“Горит ли Париж?”
киноверсия бестселлера
об освобождении Парижа осенью
1944, открывается в Нью-Йорке 9 ноября.
Мало кто вспомнит, что

ноября имеет зловещий
запах для евреев Европы; это
было 9 ноября 1938 года,
когда начались погромы при
Гитлере — не дата, чтобы
праздновать.
“Горит ли Париж?” был произведен покойным Полом Грецем и
.0012, режиссер француз Рене Клемент-
. Ожидается участие в
гала-открытии звезды
Жан-Поль Бельмондо, Шарль
Буайе, Кирк Дуглас, Лесли Ка-
Рон, Жан-Пьер Кассель, Джордж
Чакирис, Ален Делон, Гленн

ГОЛЛИВУД — Далия Лави,
, актриса израильского происхождения, чьи
главных ролей в американских фильмах
включают Колумбийский «Лорд Джим» и
«Глушители», была подписана
Джозефом Э. Левином на одну из главных ролей
с Лоуренсом Харви в «Девятке».0012 Шпион с холодным носом», совместное производство Para-
и посольства для
, предстанет перед камерами этим летом в Англии. В экранизации Джозефа Кона-
для шпионских триллеров Грегори сводит группу шпионов после информарада «Лорд Джим», гламурный
Пек и Софи Лорен вместе пошли как ция, а Софи Лорен с одной по секрету. – роль агента в “
играет одну из главных ролей в «Арабеске», теперь шоу, или другая группа – с Пеком Не-Глушителем, чтобы еще раз испытать
в пяти кинотеатрах Детройта – способная выяснить, является ли она соблазнительной шпионкой в ​​предстоящем
Бирмингем, Меркьюри, Ма – “хороший парень” или “плохой парень” до фильма. Комедия международного
гребня Mall Cinema, Vogue и Wy – самый финал. Генри Манчини – интрига, действие которой происходит в Лондоне и Мос-
Андотте. Как американская биржа, ответственная за мелодию коровы, “Шпион с холодным носом”
Профессор Оксфорда, Пек выбран из фильма, который Стэнли Донен продюсирует Леонард
под руководством банды арабских шпионов, чтобы разгадать направленный и продюсированный для Универ-Лайтстоун и режиссер Даниэль
Петри по оригинальному сценарию
a криптограмма спрятана в группе сал.
Рэя Гальтона и Алана Симпсона.
Это будет второе предприятие
для Лайтстоуна и Петри, которые
сотрудничали с недавним
дантистом,

был
играя
игра

ДЖЕССИ СИЛВЕР
завершил «Идол» с Джен-
в главной роли с 1927 года и говорит, что больше не будет
(Авторское право, 1966, JTA, Inc. )
Нифер Джонс, Майкл Паркс и
Недавно завершил восьмую шину на тренировке еще 10 Джона Лейтона в Лондоне.
Играм в Хапоэле в Израиле исполнилось 700 лет.
* *
Эйлин Эпштейн из Бостонского университета-
спортсменов из 22 стран плюс
Гила
Голаны,
наши
второй израильтянин
800 израильтян. На церемонии открытия присутствовала одна из четырех женщин
nies на стадионе в Рамат-Гане, финалисты, которые соревновались в Na- фаворите, в Европе в турне
собрали толпу из 30 000 человек, включая межвузовский бильярд 20th Century – Fox «Наш человек
» с президентом Шазаром. Среди проведенных турниров недавно в Ми-Флинте», в котором она тоже изобразила
наций, представленных на Играх ami U. во Флориде. Мисс Эпштейн, ловкий секретный агент (кто не
в наши дни?) почти встретилась с теми же
в Польше, Венгрии, Чехословакии — юниорка, занявшая третье место.
судьба как Айседора Дункан — в
ли
Эйлин
нравится
на
играть
бил-
вакия. Румыния и Югославия.
Русские однако не смогли лжецов? «Я должна быть старшей», — сказала она Роме. В фотостудии фигурирует
. Игры были открыты для допуска. «Но у них не было I pher Pierluigi, Gila позировала в
еврейских и нееврейских бильярдах в Бостонском университете, пока я не надела розовое шифоновое вечернее платье с
на первом курсе. Так что я осталась длиной в пол. шарф, который она завернула
лет.
из школы в год.” на ее шее. У Пьерлуиджи было
Выдающаяся производительность
установила электрические вентиляторы с каждой стороны
израильтянин был повернут в нее винтовкой
вне поля зрения камеры, чтобы получить
стрелок N ‘ hemia Sirkiss. Он
эффект ветра. Шарф
сравнялся с мировым рекордом от ‘Blue Max Brings
концов, застрявших в вентиляторах, разорвал
лежачих положений, когда он получил
Историю Первой мировой войны, чтобы экранировать их, и чуть не задушил ее до
398 баллов из сносных 400.
• смерть
до

пробки были вытащены
пролет
из
четырехлетний
Во время

американцы захватили корзину-
, чтобы остановить вращение.
турнир по мячу во время Первой мировой войны в Джорджтауне, введение
* * *
Колледж Кентукки выиграл последнюю воздушную мощь в войне, принес
Марти
Аллен,
, который говорит, что его_
из
человек,

породы
о

новый
от Hapoel 77-71.
Премьер-министр Израиля Леви Эшколь, летчик-истребитель, смельчак, чья семья приехала с юга в
самый ранний “Южная Польша” и его латинский
присутствовали на церемонии закрытия дуэли в воздухе в
партнер Стив Росси дико мчался
в Хайфе, где формы Hamel Sports самолетов.
вокруг Лос-Анджелеса на вертолете
Организация была основана 40 лет
История
и лимузина в прошлые выходные до
назад.
один из них
начало первого из двух дней
Ларри Хендельсман из Rochester wingedWarriors
интенсивные личные выступления на
U. привели свою команду к титулу в 20-м
автомобилей и театров, имея
Легкая атлетика штата Нью-Йорк.
Century-Fox совершил поездку по восемнадцати городам из чемпионата Phila-
Association. Хан — «Синий Макс»,
, Делфия, Нью-Йорк — Вашингтон —
делсман захватил 440 и 880 в цвете, с
тоннами в главных ролях, округ Колумбия, Бостон и Шарлотта,
, и пробежал ногу на выигрышном 440 Джордже Пеппарде,
Южная Каролина совместно с эстафетными командами
и mile. . . Хотя Джеймс Мейсон, Ур-
, начало «Последнего из
не победитель. Брюс Селман из Sula Andress, Jer-
Secret Agents?» — сумасбродная комедия
Нью-Йоркского университета, впечатленная во внешней политике Кемпа, и
edy, наполненная визуальными уловками
Metropolitan Collegiate Karl Michael
, но довольно слабо написанная. ..
Чемпионшинк Селм занял место Фоглера, который опередил
Нэнси Синатру, Джона Уильямса и
вторым в миле за 4:18.0 и зарезервировал его
Лу Якоби (наш друг со времен “
” занял третье место в миле участие в двухмильном сидении
Дневник Анны Франк”) поддерживаются
с хронометражем 9:30,4. Еще один на Саммите
портирует дурацкую комедийную команду в
Первокурсник Нью-Йоркского университета Дэн Розен взял Theatre Wednes-
их дебют в кино.
секунда в 880 в 1:55.1 и пробежал день
Мейсон
*
*
нога на эстафете победной мили
Сценарий Джеральда Хана-
Джерри Льюис подписал новый,
Барри Либовиц из Майами выиграл Лей, Дэвид Персолл и Джек Сед –
Средняя школа штата Флорида 440 дон основана на самой продаваемой неэксклюзивной сделке с Columbia
титул, когда он пробежал 48,9. Либовиц был одноименным романом Джека, который делал одну картину в год в течение
нераскрытых периодов. Льюис будет
большую часть гоночного сезона с
Д. Хантером.
функционируют четырьмя способами: как писатель, про-
мышечная тяга. Он, наверное,
Пеппард, один из самых
дюсеров, режиссеров и звезд. Работа
посещают младший колледж Майами-Дейд
сложные роли в его карьере
название его первого под 1966/67
Юг в следующем году. Либовиц изображает неустанно амбициозного молодого человека.Пакт 0012 – это «Сын спасательной шлюпки», а
опустил свою победу в штате, набрав
листовок. В дополнение к драме маловероятное название для истории фарса
49,1 на следующей неделе. . . Уолт Ли-
истерзанного войной неба, фильм «Фа-
», написанный Льюисом в сотрудничестве с «
» из Майами-Бич, получил ругательства Дейда
за личную историю
с Биллом Ричмондом. В среднем –
округов 440 титулов с 49,8. Он
роман Пеппарда с Ур-
время, Джерри Льюис “Трое на
может принять участие в Университете Оклахомы
Сула Андресс, чья роль в «
Диване» создана для . Колумбия в
в следующем сезоне.
Синий
Макс”
– это
значительно
больше
1965, в котором он играет одну из главных ролей с
Брюсом Коэном, старшим в Корнелле,
привел Большой Красный в Лигу Плюща требовательнее, чем кто-либо другой она израильтянка Гила Голан, примерно
открыт в Нью-Йорке
лакросс название Коэн, нападение- еще не эссе
Название фильма относится к
* *
человек из Болдуина, штат Нью-Йорк, также
выиграл корону плюща с синей эмалью и серебряную медаль —
Мейер Левин возвращается в Исро!эль в
28 очков. Он был плющом, завоевавшим немецкую «Pour le Merite» — июль, чтобы снять его оригинальную историю,
высшую награду, которую «Гор и Игорь» в своем подлинном
лидере в 1964 году.
Коэн, 5 футов 8 дюймов, 175
tic сеттинг с Питером Фраем direct-
Ирландия была выбрана в качестве места ing.0012 студент инженерного факультета, который также играет
в футболе. Корнелл установил ничью в сложной постановке, так как его с русским интеллектуалом на
за титул, победив Принстонскую местность, поразительно похоже на тур по культурному обмену в Near
8-7, когда Коэн забил пять голов. районы Соммы Франции как Восток и с foiksinger из
Последний выиграл игру, как это было в 1918 году; тем не менее, именно в Соединенных Штатах, которые пропустили
, пришли всего за две минуты и легко добраться до линий связи, страна, чтобы избежать морали
Осталось 40 секунд. В финале катионы и его небеса не являются зарядами. Оба встречаются в Израиле
против Дартмута, Коэн забивает голы из рекламы и частных лиц для нашего удовольствия. Новый
Левина дважды и имел семь ассистов, так как летал, и воздух не был забит романом _ “Крепость”, значит
смогом, туманом или загрязнением.
в то время как выиграл Дарофф 1966 года
Корнелл выиграл 21-5.
За эпизоды воздушного боя в призе за лучший еврейский роман-
Доктор Бернард Шенбаум из
Нью-йоркский клуб лакросса доказывает фильм, девять дотошно воссоздающих интерес. * * *
каждый раз, когда он играет, что лакроссы самолетов Первой мировой войны были
Сид Цезарь завершил свой
не обязательно построенный молодым человеком примерно за
главных ролей в игре Билла Каса-
. Шенбаум, 54 года, 250 000 долларов.

Выдающиеся достижения в спорте

Форд, Э. Г. Маршалл, Ив Монтан-
, Симона Синьоре, Пол Стэк
и денацифицированное золото Германии-
палец — Герт Фробе, последний
изображает «хорошего» генерала
Вермахта, который защищает Париж
от сожжения фюрером.
*
*

“Похороны в Берлине” из
той же Paramount Studios, превращает
из хорошего немца прошлого-
года в плохого россиянина сегодняшнего дня.
Это остросюжетная история британского агента
, посланного в Берлин, чтобы
организовать перебежку высокопоставленного московского
чиновника с Востока • на
Запад. Майкл Кейн изображает 9Агент 0012 Гарри Палмер, созданный им
в «Файле Ипересс».
россиянин — Оскар Хомолка. Женский интерес
вызван очаровательной немкой
Евой Ренци в роли агента
под прикрытием Саманты Стил.
Гай Гамильтон режиссирует Гарри
Зальцмана, человека, который подарил нам —
Джеймса Бонда.

ПО НАРОДНОМУ СПРОСУ !

Сейчас бронирование —

ЭД БУРГ

и его оркестр
Хорошая музыка
на все случаи жизни

LI 4-9278

АРЕНДА

Новый Continental Mohair

Tony Martin Dress Suits

также включает в себя прекрасный выбор

Мужская одежда
Дисконтные цены

Handelsman Clothing

7651 W. McNichols At Santa Barbara
Университет 4-7408

9

W. McNichols At Santa Barbara
Университет 4-7408

2

W. McNichols At Santa Barbara
Университетский
КОСТЮМЫ
С ROYAL Fit

IRV

СКАЖИ ПАПЕ. . .
МЫ ТОЖЕ МОЖЕМ ЕГО ПОДХОДИТЬ!!

SOL

PRINCETON SHOP

Для мужчин
и мальчиков
от 6 до 60

7 миль в вечнозеленой-аспекты бесплатной парковки
Приглашенные счета заряда
KE 3-4310

AIIIIIIMERMINUEMPIENV

CVS до M F-1CDIN/1

—

EB

2_JIL_JIL_JIL_IR_JIL_JIL_IR_JIL_IR_JIL_IR_JIL_IR_JIL_IIL_IR_IIL_IIL_IIL_IIL_IIN_IR_JIL_IIL_IR_JIL_IIL_IR_JIL_IR_JIL_IR_JIL_IR_JIL_JIL_IR_JIL_IILIN/10006

– = ItV EBL—CDC>1 ■ ./11L_EMD,

Используйте наш дизайн дома или свой собственный
NORMAN N. SNYDER LEOPOLD J. SNYDER

Отдел продаж

Строительство и проектирование

Телефон:

2 863-9629 Реконструкция общих эллиптических поверхностей K3 из пределов Громова-Хаусдорфа – arXiv Vanity

Кендзи Хашимото Высшая школа математических наук, Токийский университет, 3-8-1 Комаба, Мегуро-ку, Токио, 153-8914, Япония. и Казуши Уэда Высшая школа математических наук, Токийский университет, 3-8-1 Комаба, Мегуро-ку, Токио, 153-8914, Япония.

Аннотация.

Покажем, что общая эллиптическая поверхность K3 с сечением однозначно определяется своим дискриминантом, которая представляет собой конфигурацию из 24 точек на проективной прямой. Отсюда следует, что общая эллиптическая поверхность К3 с сечением может быть восстановлен по его пределу Громова–Хаусдорфа когда объем волокна стремится к нулю.

1. Введение

Пусть f,g∈\bC[z,w] — однородные многочлены степени 8 и 12 соответственно, и определим полином h степени 24 с помощью

(1)

ч=f3+g2.

В этой статье мы показываем следующее:

{теорема}

Если f и g являются общими, тогда разложение h в сумму куба и квадрата однозначно, вплоть до очевидной двусмысленности умножения на кубический и квадратный корень из единицы.

Заметим, что соответствующая задача теории чисел имеет неединственные решения в общем случае. Есть три решения

(2)

13+42

=23+32,

13+82

=43+12,

23+92

=43+52

для натуральных чисел меньше 100, и

(3)

13+322=43+312=53+302=103+52

— наименьшее целое число что можно записать в виде суммы куба и квадрата более чем двумя способами. Эллиптическая кривая вида

(4)

у2=х3+n

для ненулевого целого числа n известна как кривая Морделла , и изучается много лет.

Задача разложения по полю функции не уникальна если f и g не являются общими. Например, для однородных многочленов u и v степени 4, у одного

(5)

4(ув)3+(ув(у-в))2

=03+(ув(и+в))2.

Эллиптическая поверхность К3 с сечением имеет модель Weierstrass

(6)

y2=4×3−g8(z,w)x−g12(z,w)

в \bP(4,6,1,1), где g8(z,w) и g12(z,w) — однородные многочлены по z и w степени 8 и 12 соответственно. Дискриминант равен

(7)

Δ=g38−27g212,

, который является однородным многочленом степени 24. Проблема разложения спрашивает если g8 и g12 можно восстановить от Δ. Наш интерес к этой проблеме связан с зеркальной симметрией. Показано в [GW00, GTZ16] что последовательность метрик Кэлера–Эйнштейна на эллиптической поверхности K3 с фиксированным диаметром сходится в топологии Громова–Хаусдорфа к сфере со структурой Монжа–Ампера с особенностями, если объем волокна стремится к нулю. Поскольку дополнение дискриминанта эллиптической поверхности K3 как проколотая сфера Римана может быть реконструирован как конформный класс гладкой части предельной метрики, \prefth:main позволяет восстановить (якобиан) общей эллиптической поверхности K3 из предела Громова–Хаусдорфа.

Этот документ организован следующим образом: В \prefsc:поверхности, поставим в соответствие вспомогательную эллиптическую поверхность X общего вида с полиномом h=f3+g2∈\bC[z,w] степени 24. В \prefsc:ро, мы показываем, что число Пикара X равно 4 если f и g очень общие. В \prefsc:доказательство, мы даем доказательство \prefth:main. В \prefsc:зеркало, мы обсуждаем связь с зеркальной симметрией для K3-поверхностей.

Благодарности

Мы благодарим Юичи Нохару за неопубликованное сотрудничество о компактификациях Громова–Хаусдорфа модулей поверхностей K3, которые привели к настоящей работе. Мы также благодарим Юдзи Одаку и Йошики Осиму. для обмена идеями и результатами о компактификациях Громова–Хаусдорфа модулей K3-поверхностей. K. H. был частично поддержан грантами в помощь научным исследованиям. (17К14156). К. У. была частично поддержана грантами для научных исследований. (24740043, 15КТ0105, 16К13743, 16H03930).

2. Эллиптическая поверхность

Пусть \Xbar — гиперповерхность степени 24 в \bP(8,12,1,1) определяется

(8)

у2=-х3+ч.

Имеет факторсингулярность типа \bC2/\la14(1,1)\ra в [x:y:z:w]=[−1:1:0:0] поступающие из окружающего пространства. Исключительный дивизор σ0 минимального разрешения X→\Xbar является (−4)-кривой. Zw-проекция \pibar:\Xbar⇢\bP1 индуцирует эллиптическое расслоение π:X→\bP1 такое, что σ0 — сечение.

Пусть e — гладкий слой π, который является полным преобразованием гиперплоского сечения \Xbar. Подрешетка U в \PicX порожденные e и σ0 — гиперболическая унимодулярная решетка ранга 2.

Обратите внимание, что КХ=ОХ(2е). Любое сечение σ многоугольника π имеет самопересечение −4 с

(9)

\cNσ/X=\cOσ\lbKσ−KX|σ\rb=\cOσ(−2−2)=\cOσ(−4).

Если σ не пересекает σ0, то есть σ2=−4, σ⋅σ0=0, и σ⋅е=1, так что

(10)

τ(σ)\coloneqqσ−σ0−4e

удовлетворяет τ(σ)⊥U и τ(σ)2=−8.

Эллиптическое расслоение π имеет шесть сечений

(11)

σ1:(x,y)=(f,g),σ2:(x,y)=(ζ3f,g),σ3:(x,y)=(ζ23f,g),σ4:(x,y) =(f,−g),σ5:(x,y)=(ζ3f,−g),σ6:(x,y)=(ζ23f,−g)

не пересекаются с σ0, где ζk\coloneqqexp\lb2π√−1/k\rb для натурального k. Пусть M — подрешетка \PicX порожденный τi\coloneqqτ(σi) для i=1,…,6.

{лемма}

Пара (τ1,τ2) является упорядоченным базисом M с матрицей Грама \квмат-844-8.

Доказательство.

Вытекает из

(12)

σ1⋅σ4=град=12

та

(13)

(τ1+τ4)2=0

и, следовательно,

(14)

τ1+τ4=0

, так как U⊥⊂\PicX отрицательно определена по теореме Ходжа об индексе. Сходным образом, следует из

(15)

σ1⋅σ2=σ2⋅σ3=σ1⋅σ3=degf=8

та

(16)

(τ1+τ2+τ3)2=0

и, следовательно,

(17)

τ1+τ2+τ3=0.

Также τ2+τ5=τ3+τ6=τ4+τ5+τ6=0, так что {τ1,τ2} — базис M. Из \prefeq:sigma12 также следует, что

(18)

τ1⋅τ2

=4,

и \preflm:M доказано. ∎

3. Число Пикара X

Пусть р(Х) быть числом Пикара X. В этом разделе мы докажем следующее:

{предложение}

Для очень общих f и g, один имеет ρ (X) = 4.

Доказательство.

Рассмотрим семейство \cY эллиптических поверхностей с параметрами a,b∈\bC, определенными как

(19)

f=aw8,g=w\lbz11+bw11\rb.

Есть

(20)

ч=f3+g2=w2\lbz11−a′w11\rb\lbz11−b′z11\rb,

где a′,b′∈\bC определяются формулой

(21)

а’+b’=-2b,a’b’=a3+b2.

Дискриминант эллиптического расслоения задается h3, который представляет собой конфигурацию (не обязательно различных) 48 точек. Семейство \cY не изотривиально, так как конфигурация зависит от параметра, даже после выделения \PGL(2,\bC)-действия. Общий член Y этого семейства имеет особый слой Кодаиры типа IV в точке [z:w]=[1:0], состоящая из трех линий, сходящихся в одной точке, так что у одного

(22)

ρ(Y)≥4+2=6.

Поскольку дискриминант имеет степень 48, топологическое число Эйлера Y равно 48, откуда следует, что второе число Бетти Y задается выражением 48−2=46. Поскольку Y — взвешенная проективная гиперповерхность, метод Гриффитса-Дворка (см., например, [Dol82] ) показывает

(23)

h3,0(Y)=2⨁i=0\bCOi,

где

(24)

Ωi=\ResY\lbziw2−i8xdy∧dz∧dw−12ydx∧dz∧dw+⋯x3+y2−h\rb

для i=0,1,2. Отсюда \bZ/33\bZ-действие, порожденное

(25)		α	:[x:y:z:w]↦[ζ3x:y:z:w],
(26)		β	:[x:y:z:w]↦[x:y:ζ11z:w]

удовлетворяет

(27)

α∗Ωi=ζ3Ωi,β∗Ωi=ζi+111Ωi.

Пусть V неприводимое представление \bZ/33\bZ над \bQ с собственными значениями \lcζj33\rc(j,33)=1. Надо dimV=ϕ(33)=20, где ϕ — тотиентная функция Эйлера. Это следует из \prefeq:action_Omega что h3(Y,\bQ) содержит V⊕k для некоторого k≥1. Если k=1, то h3,0(Y) не зависит от параметров a и b, что противоречит неизотривиальности семейства \cY и локальная теорема Торелли для эллиптических поверхностей [Кий78, Ча84, Сай83] . Следовательно, k=2, что подразумевает

(28)

ρ(Y)≤46−dimV⊕2=6,

, так что ρ(Y)=6 для очень общего Y.

Теперь пусть X будет эллиптической поверхностью определяется очень общими f и g, так что любой особый слой имеет тип I1 и ρ(X)≤6. Предположим, что ρ(X)=6. Противоречие. Тогда существует деформация X в Y такая, что h3,0(X)⊂V⊕2⊗\bC под индуцированной идентификацией h3(X;\bZ)=h3(Y;\bZ), что подразумевает \PicX=\PicY. Пусть d — (−2)-вектор в \PicY исходящие из единственного волокна типа IV. Теорема Римана–Роха показывает

(29)		χ(\cOX(d))	\coloneqqh0(\cOX(d))−h2(\cOX(d))+h3(\cOX(d))
(30)			=12d. (d-KX)+112(K2X+c2(X))
(31)			=12d2+112c2(Х)
(32)			=−1+4812
(33)			=3,

, так что действует либо d, либо KX-d=-d+2e. Поскольку d ортогонален e и каждый особый слой X неприводим, делитель d должен быть кратен e, что противоречит d2=−2 и e2=0.

Далее предположим от противоречия, что ρ(X)=5. Тогда \PicX⊗\bQ генерируется над \bQ с помощью U, M и δ с α∗δ=δ. По теории эллиптических поверхностей [Shi90] группа Морделла–Вейля X есть изоморфен

(34)

\Pic(X)/(U+(решетка, порожденная неприводимыми компонентами сингулярных % волокна)).

Следовательно, класс δ соответствует α-инвариантному сечению отличается от σ0. Такое сечение задается x=0 и y=ψ для однородного многочлена ψ по z и w степени 12 удовлетворяющие ψ2=h. Существование квадратного корня ψ из h противоречит предположению что f и g очень общие, и ρ(X)=4 доказано. ∎

4. Доказательство основной теоремы

В этом разделе мы докажем \prefth:main. Сначала докажем единственность разложения для очень общих f и g. Для любых элементов φ и ψ в \bC[z,w] степени 8 и 12 удовлетворительно

(35)

ч=φ3+ψ2,

сечение σ определяется формулой (x,y)=(φ,ψ) не пересекает σ0, так что τ(σ)∈U⊥⊂\PicX. Для очень общих f и g один имеет ρ(X)=4, и, следовательно, τ(σ)∈M⊗\bQ. Напомним, что матрица Грама упорядоченного базиса (τ1,τ2) M это \sqmat-844-8. Непосредственным вычислением можно увидеть это нет элементов ρ∈M⊗\bQ такое, что ρ.M⊂\bZ и ρ2=−8 кроме τ1,…,τ6, а единственность разложения следует из того, что группа Морделла–Вейля X естественно изоморфна \Pic(X)/U≅(M⊗\bQ)∩\Pic(X).

Чтобы доказать единственность разложения для общих f и g, пусть S и T — подпространства в \bC[z,w] состоящая из однородных полиномов 8 и 12 степени соответственно, и определить подсхему Z из (S×T)2 с помощью

(36)

Z\coloneqq\lc((f,g),(φ,ψ))∈(S×T)2\relmidf3+g2=φ3+ψ2\rc.

Единственность разложения для очень общих f и g означает, что первая проекция Z→S×T, который является морфизмом схем, обычно шесть к одному. Следовательно, первая проекция шесть к одному вне замкнутого подмножества Зарисского, и \prefth:main доказано.

5. Зеркальная симметрия для поляризованных тропических поверхностей K3

Предполагают Строминджер, Яу и Заслоу. [SYZ96] что любое многообразие Калаби – Яу имеет специальное лагранжево расслоение на тор, а зеркальное многообразие получается как дуальное специальное лагранжево торовое расслоение. Это изображение было доработано в [GW00, KS01] к гипотезе о том, что метрика Калаби–Яу с диаметром, приведенным к единице сходится в топологии Громова–Хаусдорфа к многообразию Монжа–Ампера с особенностями по мере приближения к большому пределу сложной структуры. Вот, Многообразие Монжа–Ампера с особенностями является многообразием B с подмножеством B\sing хаусдорфовой коразмерности 2 такое, что B∖B\sing имеет тропическую аффинную структуру (т.е. атлас, функции преобразования которого находятся в \GLn(\bZ)⋉\bRn) и метрика Монжа–Ампера (т.е. риманова метрика формы Гессе

(37)

gij=∂2K∂xi∂xj

в аффинной координате удовлетворяющий det\lb\lbgij\rbi,j\rb=константа). Появляется многообразие Монжа-Ампера. с двойной парой аффинных структур, и зеркальная симметрия должна их поменять местами.

В случае поверхности K3, специальное лагранжево расслоение на тор можно превратить в эллиптическое расслоение гиперкелеровым вращением. Показано в [GW00, GTZ16] что последовательность метрик Калаби–Яу на эллиптической поверхности K3 с фиксированным диаметром сходится в топологии Громова–Хаусдорфа к сфере со структурой Монжа–Ампера с особенностями когда объем волокна стремится к нулю. Предельную сферу B естественно отождествить с основанием \bP1 эллиптической поверхности K3, и дискриминант B\sing структуры Монжа–Ампера можно отождествить с дискриминантом эллиптической поверхности K3. Под этим отождествлением метрика Монжа–Ампера g на B∖B\sing пишется как

(38)

г=I\lb\taubar1τ2\rbdz⊗d\zbar,

где z — голоморфная локальная координата на базе \bP1 и (τ1,τ2) – периоды, по симплектическому базису, относительной голоморфной формы λ на эллиптическом расслоении двойственно к dz относительно голоморфной объемной формы поверхности K3. Отсюда следует, что комплексная структура базы \bP1 минус дискриминант можно восстановить по предельной метрике, вплоть до выбора направления. Обратите внимание, что метрика \prefeq:MAS2 зависит только от расслоения Якоби, так что можно считать, что эллиптическая поверхность К3 имеет сечение. Из \prefth:main следует, что общая эллиптическая поверхность K3 с сечением можно восстановить по предельной метрике до комплексного сопряжения.

Эллиптическая поверхность К3 с сечением соответствует к K3-поверхности, поляризованной унимодулярной гиперболической решеткой U второго ранга в смысле Никулин [Nik79] . По глобальной теореме Торелли и сюръективности отображения периодов пространство модулей U-поляризованных K3-поверхностей описывается как частное

(39)

\lcΩ∈\bP(Λ2,18⊗\bC)\relmid(Ω,Ω)=0, (Ω,\Omegabar)>0\rc/\rO(Λ2,18),

где Λ2,18≅E8⊥E8⊥U⊥U является четной унимодулярной решеткой подписи (2,18). Комплексное сопряжение поверхности K3 соответствует комплексному сопряжению периода, который меняет местами действительную часть и мнимую часть периода;

(40)

Ом=ω1+√−1ω2↦−√−1\Омегабар=ω2+√−1ω1.

Пространство модулей тропических аффинных структур на S2 с 24 особенностями фокус-фокус является хаусдорфовым орбифолдом размерности 44, на котором есть слоение коразмерности 20 [KS06, раздел 6. 7.1] . Каждый лист соответствует тропическим аффинным структурам с фиксированной обструкцией лучистости, а нехаусдорфово пространство листов равно

(41)

\lcv∈Λ2,18⊗\bZ\bR\relmid(v,v)>0\rc/O(Λ2,18).

\преф

eq:mtropK3 — тропический аналог нехаусдорфова пространства модулей

(42)

\lcΩ∈\bP(Λ3,19⊗\bC)\relmid(Ω,Ω)=0, (Ω,\Omegabar)>0\rc/\rO(Λ3,19)

поверхностей К3, тогда как \prefeq:mptropK3 является тропическим аналогом помещения

(43)

\SO(Λ3,19)∖\SO0(3,19)/\SO(3)×\SO(19)

риччи-плоской кэлеровой (орби-)метрики на поверхностях К3 [КТ87] . И действительная часть ω1, и мнимая часть ω2 периода \prefeq:Omega дать очки в \prefeq:mtropK3, которые меняются местами комплексного сопряжения. При вращении гиперкэлера используется для преобразования специального лагранжевого расслоения на тор на эллиптическое расслоение, один из них происходит от формы Кэлера а другой исходит из (действительной части) голоморфной объемной формы. Это мотивирует нас назвать сферу, оснащенную структурой Монжа–Ампера с особенностями и ориентация поляризованная тропическая поверхность K3 . Он имеет комплексную аффинную структуру . с периодом ω1 и симплектическая аффинная структура с периодом ω2. Обмен этими двумя периодами является тропическим аналогом Зеркальная симметрия Аспинуолла-Моррисона для поверхностей K3, который обменивает голоморфная объемная форма и комплексная кэлерова форма в решетке Мукая Λ4,20.

Есть и тропические аналоги зеркальной симметрии Долгачева. Напомним, что пара M и \Mv решеток сигнатур (1,ρ−1) и (1,\rhov−1) говорят, что K3-двойной друг к другу если их можно одновременно встроить примитивно в Λ2,18 таким образом, что они являются ортогональными решетками друг друга. В этом случае, пространство модулей

(44)

\lcΩ∈\bP((\Mv⊥U)⊗\bC)\relmid(Ω,Ω)=0, (Ω,\Omegabar)>0\rc/\rO(\Mv⊥U)

М-поляризованных поверхностей К3 и пространство модулей

(45)

\lcΩ∈\bP((M⊥U)⊗\bC)\relmid(Ω,Ω)=0, (Ω,\Omegabar)>0\rc/\rO(M⊥U)

\Mv-поляризованных поверхностей К3 называются пространствами зеркальных модулей в смысле Долгачева [дол96] . Тропические аналоги \prefeq:Mpol и \prefeq:Mvpol:

(46)

\lcv∈\bP(\Mv⊗\bR)\relmidv2>0\rc/\rO(\Mv)

и

(47)

\lcv∈\bP(M⊗\bR)\relmidv2>0\rc/\rO(M),

, которые образуют тропические аналоги пространств зеркальных модулей. Это направление мысли, вместе с произведениями Одаки [Одаа, Одаб] о компактификациях Громова–Хаусдорфа пространств модулей, приводит к идее компактификации пространства модулей \prefeq:Mpol решетчато-поляризованных поверхностей К3 добавив \prefeq:Mpoltrop до порога. Эта идея была реализована частично в особых случаях в [HNU] , и самостоятельно и более подробно в [OOa, OOb] 905:30 , где обнаруживается связь с компактификацией Сатаке. Для антиканонических гиперповерхностей в трехмерных торических многообразиях Фано Yamamoto [Yam] вычислил тропический аналог карты периодов, который принимает значения в (числителе) \prefeq:Mpoltrop.

Ссылки

• [Ча84] Кен Чакирис, Задача Торелли для эллиптических карандашей , Темы в трансцендентальная алгебраическая геометрия (Принстон, Нью-Джерси, 1981/1982), Ann. из Мат. Студ., вып. 106, Принстонский университет. Press, Принстон, Нью-Джерси, 19 лет.84, стр. 157–181. МР 756851
• [Дол82] Игорь Долгачев, Взвешенные проективные многообразия , Групповые действия и вектор поля (Ванкувер, Британская Колумбия, 1981), Lecture Notes in Math. , vol. 956, Springer, Берлин, 1982, стр. 34–71. МР 704986
• [дол96] И. В. Долгачев, Зеркальная симметрия для решетчато-поляризованных К3-поверхностей , Дж. Матем. науч. 81 (1996), вып. 3, 2599–2630, Алгебраическая геометрия, 4. МР 1420220 (97i:14024)
• [ГТЗ16] Марк Гросс, Валентино Тосатти и Югуан Чжан, 9 лет0475 Громов-Хаусдорф схлопывание коллекторов Калаби-Яу , Комм. Анальный. геом. 24 (2016), нет. 1, 93–113. МР 3514555
• [GW00] Марк Гросс и П. М. Х. Уилсон, 90 475 Ограничения большой сложной структуры K3 поверхности , Ж. Дифференц. геом. 55 (2000), вып. 3, 475–546. MR 1863732 (2003a:32042)
• [ХНУ] Кенджи Хашимото, Юичи Нохара и Казуши Уэда, неопубликованные.
• [Кий78] К. И. Кий, Локальная теорема Торелли для многообразий с делимым канонический класс , Изв. акад. АН СССР сер. Мат. 42 (1978), вып. 1, 56–69, 214. МР 0499325.
• [КС01] Максим Концевич и Ян Сойбельман, Гомологическая зеркальная симметрия и тор расслоения , Симплектическая геометрия и зеркальная симметрия (Сеул, 2000), Мир науч. Publishing, Ривер Эдж, Нью-Джерси, 2001 г., стр. 203–263. МР MR1882331 (2003c:32025)
• [КС06] того же автора, Аффинные структуры и неархимедовы аналитические пространства , The единство математики, прогр. Матем., вып. 244, Биркхойзер Бостон, Бостон, Массачусетс, 2006, стр. 321–385. МР MR2181810
• [КТ87] Риоичи Кобаяши и Андрей Н. Тодоров, 90 475 Поляризованная карта периода для обобщенные K3-поверхности и модули метрик Эйнштейна , Тохоку Мат. J. (2) 39 (1987), вып. 3, 341–363. МР
  4
• [Ник79] В. В. Никулин, Конечные группы автоморфизмов кэлерова K3 поверхности , Труды Москвы. Мат. общ. 38 (1979), 75–137. МР 544937 (81e:32033)
• [Одаа] Юдзи Одака, Тропическая геометрическая компактификация модулей, I – Mg корпус – , архив: 1406.7772.
• [Одаб] того же автора, Тропическая геометрическая компактификация модулей, II – Ag случай и голоморфные пределы — , Международные заметки об исследованиях математики, rnx293, https://doi.